线性代数
一:线性方程组
概念
- 线性方程
- 线性方程组
- 系数
- 解:一组能让方程左右相等的数
- 解集:方程组的所有解的集合
- 等价:若两个线性方程组拥有相同解集,则两者等价
- 相容:方程组有一个或无穷多个解
- 不相容:方程组无解
矩阵
方程组
$$
\begin{gathered}
x_1-2x_2+x_3=0 \\
2x_2-8x_3=8 \\
5x_1-5x_3=10
\end{gathered}
$$
的系数矩阵为
$$
\left[ \begin{matrix}1&-2&1\\ 0&2&-8\\ 5&0&-5\end{matrix} \right]
$$
增广矩阵为
$$
\left[ \begin{matrix}1&-2&1&0\\ 0&2&-8&8\\ 5&0&-5&10\end{matrix} \right]
$$
这个增广矩阵,3行4列,是一个3x4的矩阵
我们对增广矩阵进行多次矩阵运算,于是得到
$$
\left[ \begin{matrix}1&0&0&1\\ 0&1&0&0\\ 0&0&1&-1\end{matrix} \right]
$$
于是原方程有且仅有一个解$(1,0,-1)$
初等行变换
也就是行简化
-
倍加:
a=a+nb,把某行加上某一行的倍数 -
对换:
swap(a,b),把某两行对换 -
倍乘:
a *= n (n!=0),把某行所有元素乘以一个非零的数
阶梯矩阵
形如
$$
\left[ \begin{matrix}x&&&\\ 0&x&&\\ 0&0&x&\end{matrix} \right]
$$
的矩阵,被称为阶梯形
- $x$为先导元素,非零
- 若先导元素均为1,而且该列只有先导元素非零,则矩阵被称为简化阶梯形
- $x$所在的位置被称为主元位置,拥有主元的列被称为主元列
- $*$取任意值
行简化
- 任何非零矩阵都可以行简化为阶梯形矩阵
- 简化阶梯形具有唯一性
线性方程的解
对增广矩阵运用行简化,得到一个简化阶梯形
$$
\left[ \begin{matrix}1&0&-5&1\\ 0&1&1&4\\ 0&0&0&0\end{matrix} \right]
$$
对应的线性方程组为
$$
\begin{gathered}
x_1-5x_3=1 \\
x_2+x_3=4 \\
0=0
\end{gathered}
$$
- 其中$x_1,x_2$为基本变量,$x_3$为自由变量
于是可以得到线性方程组的通解
$$
\begin{cases}
x_1=1+5x_3&\\
x_2=4-x_3&\\
x_3是自由变量
\end{cases}
$$
向量方程
向量
n维向量可以写成nx1列矩阵的形式
$$
\mu=\begin{bmatrix}
1\\ 1\\ \vdots \\ 1
\end{bmatrix}
$$
- 所有元素为0的向量称为零向量
- 当且仅当两个向量对应元素全相等时,两向量相等
为了方便书写,我们会将n维向量横着写(注意!用的是括号,并且相邻元素间用逗号隔开)
$$
(1,1,…,1)
$$
向量方程
向量方程:
$$
x_1\mathbf{a_1}+x_2\mathbf{a_2}+…+x_n\mathbf{a_n}=\mathbf{b}
$$
的解,等同于增广矩阵为
$$
\begin{bmatrix}\mathbf{a_1}&\mathbf{a_2}&…&\mathbf{a_n}\end{bmatrix}
$$
的线性方程组的解
-
$Span{\nu}$
-
$Span{\nu_1,\nu_2,…,\nu_n }$
矩阵运算
$$
A\mathbf{x}=
\begin{bmatrix}\mathbf{a_1}&\mathbf{a_2}&…&\mathbf{a_n}\end{bmatrix}
\begin{bmatrix}x_1\\ x_2\\ \vdots \\ x_n\end{bmatrix}
=x_1\mathbf{a_1}+x_2\mathbf{a_2} + …+x_n\mathbf{a_n}
$$
- 当且仅当左边的列数等于右边的行数,才可以运算(横乘竖)
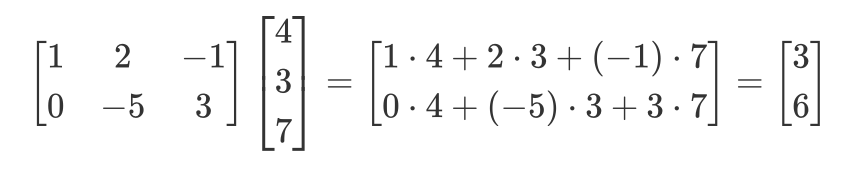
矩阵方程
$$
A\mathbf{x}=\mathbf{b}
$$
齐次线性方程组
若线性方程的常数项为0,则称该线性方程为齐次的,可以写成
$$
A\mathbf{x}=\mathbf{0}
$$
的形式
- 齐次线性方程必有一个平凡解,即$\mathbf{x}=\mathbf{0}$
- 齐次线性方程有非平凡解,当且仅当方程组至少有一个自由变量
要判断$A\mathbf{x}=\mathbf{0}$有无非平凡解
- 写出方程组的增广矩阵$[A, \mathbf{0}]$
- 将矩阵化简为简化阶梯形
- 若存在某一行全为0(该行对应的变量就是自由变量),则有非平凡解
- 哪些不全为0的行所对应的变量称为基本变量
线性无关
若线性方程仅有平凡解,则该组向量(矩阵各列)线性无关
矩阵
要判断某个矩阵各列是否线性无关:
- 写出矩阵的增广矩阵$[A, \mathbf{0}]$
- 对矩阵进行行简化
- 若矩阵没有自由变量,则说明各列线性无关
向量的集合
-
一个向量的集合线性无关的条件:当且仅当向量不是零向量
-
两个向量的集合线性相关的条件:当且仅当某个(非零)向量是另一个(非零)向量的倍数
-
多个向量的集合线性相关的条件:当且仅当至少有一个向量是其他向量的线性组合
- 若一个向量组中向量个数多于每个向量的元素个数,那么这个向量组线性相关(充分条件)
能看出,两个向量属于多个向量
线性变换
变换
$$
A\mathbf{x}=\mathbf{b}
$$
一个n维向量左乘一个m行n列的矩阵,会得到一个m维的向量
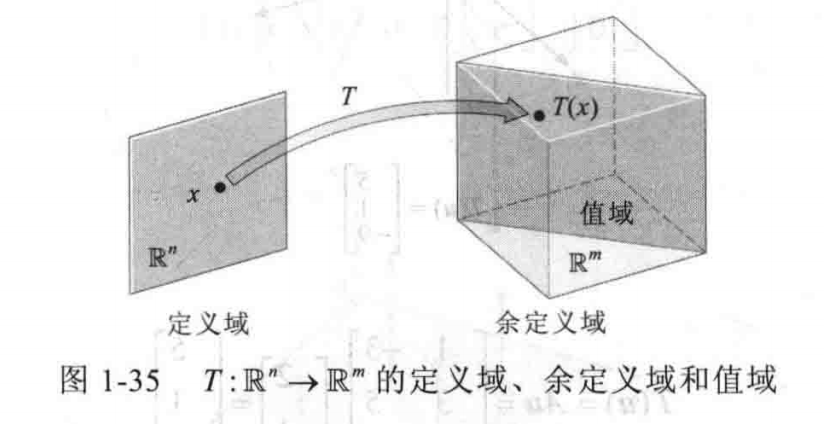
我们称$\mathrm{R}^n \rightarrow \mathrm{R}^m$这个过程为一个变换,也可以叫做函数、映射
变化的规则为$T$,$\mathrm{R}^n$被称为$T$的定义域,$\mathrm{R}^m$被称为$T$的余定义域
对于$\mathrm{R}^n$中的一个向量$x$,其在$\mathrm{R}^m$中的向量$T(x)$被称为$x$的像,所有的像的集合被称为值域
线性变换
若定义域中的一切向量满足
- $T(\mathbf{u}+\mathbf{v})=T(\mathbf{u})+T(\mathbf{v}) $
- $T(c\mathbf{u})=cT(\mathbf{u})$
则称该变换为线性变换
线性变换的性质:
- $T(\mathbf{0})=\mathbf{0}$
- $T(c\mathbf{u}+d\mathbf{v})=cT(\mathbf{u})+dT(\mathbf{v}) $
若n等于m,$T(\mathbf{x})=r \ \mathbf{x}$
- 若
r > 1,则称为拉伸变换 - 若
0 < r < 1,则称为压缩变化
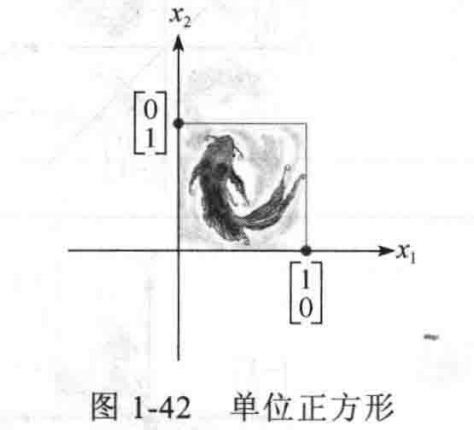
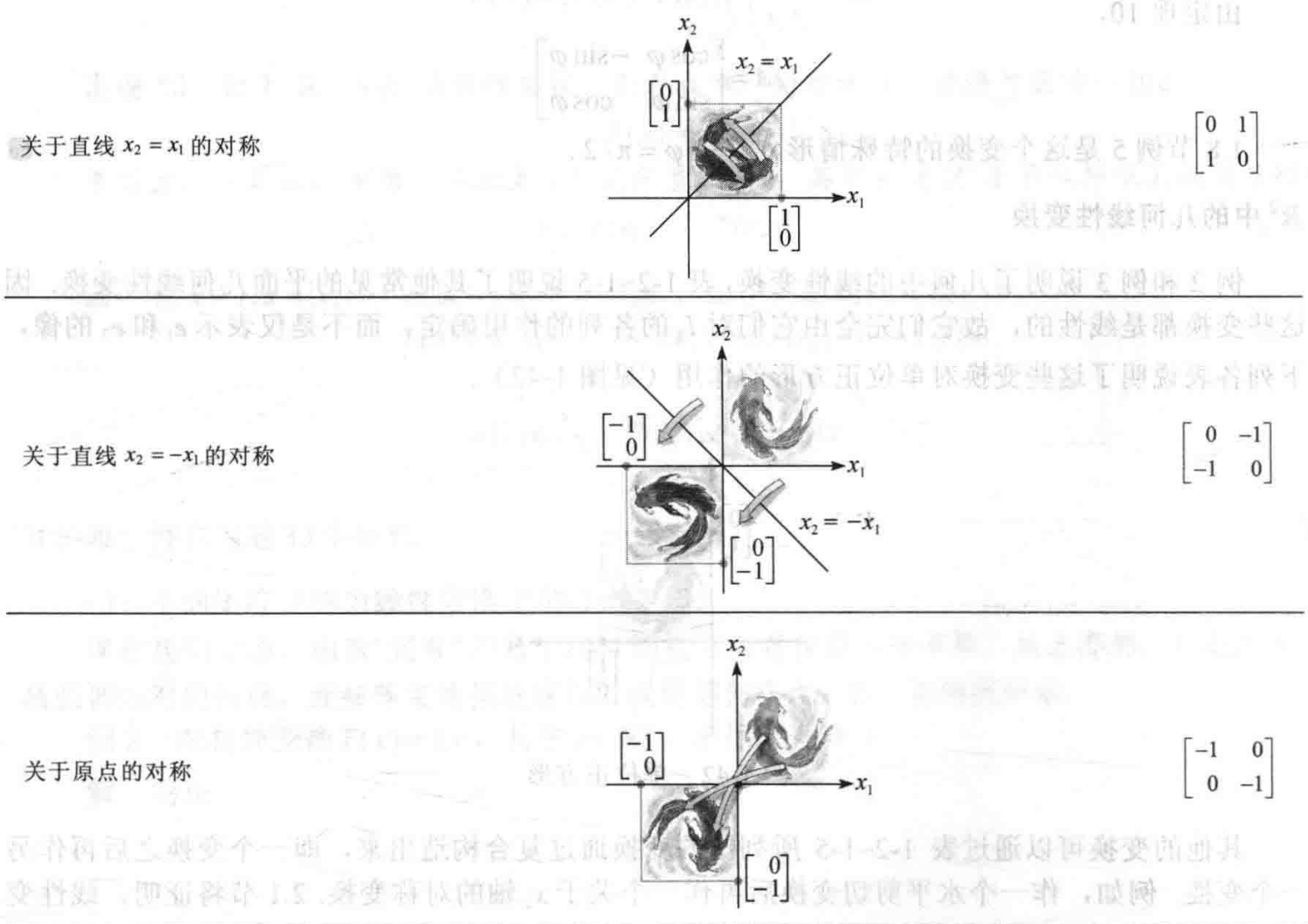
变化矩阵
二维空间的变化矩阵为,$(x_1, y_1)$为变化后单位正方形右下角的位置,$(x_2, y_2)$为变化后单位正方形左上角的位置
$$
\left[ \begin{matrix}x_1&x_2\\ y_1&y_2\end{matrix} \right]
$$
二:矩阵代数
矩阵
对于一个mxn的矩阵,也就是m行n列的矩阵,我们可以写作
$$
A=[\mathbf{a}_1 \ \mathbf{a}_2\ \cdots \mathbf{a}_n]
$$
其中
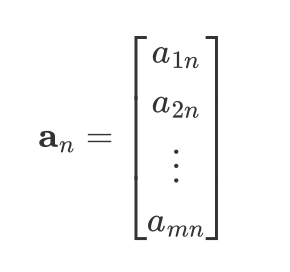
矩阵A的对角元素为$a_{11}, a_{22}, \cdots$,他们组成了矩阵A的主对角线
对角矩阵:非对角线元素全为0的矩阵
零矩阵:元素全为0的矩阵,根据其尺寸,可以写为$\mathbf{0}_{m \times n}$
矩阵运算
矩阵相等:维数相同且对应元素均相同
矩阵相加:维数相同的矩阵才能相加,结果为对应元素相加
矩阵标量乘:矩阵所有元素乘一个标量



