球函数
三大偏微分方程
- 拉普拉斯方程(椭圆)
- 热方程(抛物线)
- 波方程(双曲线)
常微分方程
含有未知函数的导数(含高阶导数)或微分的等式,称为微分方程
若未知函数是一元函数,则该函数为常微分方程
若导数的阶数为1,那么称为一阶微分方程
球坐标系
讨论常微分方程时,边界是记为重要的,而当边界是球形时,球坐标系会更好用
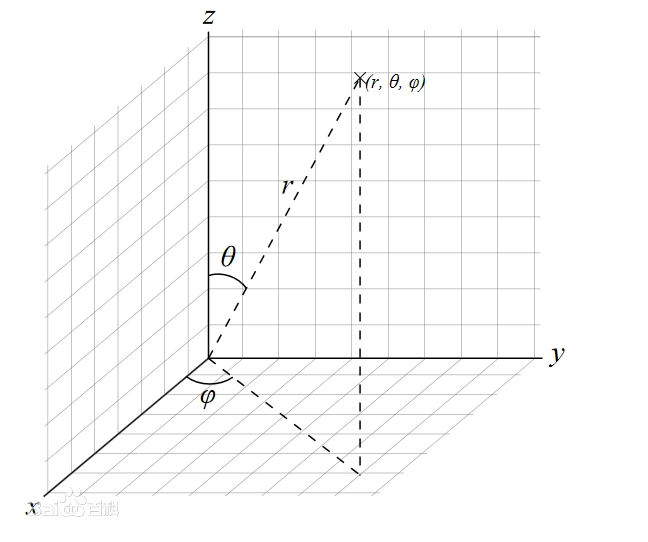
直角坐标系上点$P(x,y,z)$,也可以用三个有次序的数$(r,\theta,\varphi)$表示
$$
\begin{cases}
x=r \sin \theta \cos \varphi \
y=r \sin \theta \sin \varphi \
z=r\cos \theta
\end{cases}
$$
$$
\begin{cases}
r=\sqrt{x^2+y^2+z^2} \
\theta=\arccos \frac{z}{r} \
\varphi=\arctan \frac{y}{x}
\end{cases}
$$
拉普拉斯方程
拉普拉斯算符
多元函数用梯度表示不同方向函数值变化的速度,拉普拉斯算符$\nabla$就是对多元函数求梯度
对梯度再次做拉普拉斯算符$\nabla ^2$,就是求梯度的散度
在直角坐标系下,二阶拉普拉斯算符为
$$
\nabla^2=\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}
$$
在球坐标下,二阶拉普拉斯算法为(将xyz带入,化简得到)
$$
\nabla^2=\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial}{\partial r})
+\frac{1}{r^2\sin \theta }\frac{\partial}{\partial \theta}(\sin \theta \frac{\partial}{\partial \theta})
+\frac{1}{r^2\sin^2 \theta }\frac{\partial^2}{\partial \varphi^2}
$$
拉普拉斯方程
拉普拉斯方程$\nabla^2 u=0$,表示的物理含义是:在各个方向上(比如二维直角坐标系,就是x和y方向)加速度合为0
这意味着什么?一个不与外界进行能量交换的系统,其拉普拉斯方程为0
- 一个不受外力的系统,其整体加速度为0
- 一个不与外界传热的系统,其整体能量传播为0
- 一个理想的简谐振动
- 闭合磁场、电场
我们称拉普拉斯方程为0的函数叫做Harmonic
球坐标系下的拉普拉斯方程
函数$u(r,\theta,\varphi)$的拉普拉斯方程为
$$
\nabla^2u=\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial u}{\partial r})
+\frac{1}{r^2\sin \theta }\frac{\partial}{\partial \theta}(\sin \theta \frac{\partial u}{\partial \theta})
+\frac{1}{r^2\sin^2 \theta }\frac{\partial^2 u}{\partial \varphi^2}=0
$$
我们将距离和方向分离,得到
$$
u(r,\theta,\varphi)=R®Y(\theta,\varphi)
$$
- $R®$表示距离
- $Y(\theta,\varphi)$表示方向,被称为球函数
带入可得
$$
\frac{Y}{r^2}\frac{\mathrm{d}}{\mathrm{d} r}(r^2\frac{\mathrm{d} R}{\mathrm{d} r})
+\frac{R}{r^2\sin \theta }\frac{\partial}{\partial \theta}(\sin \theta \frac{\partial Y}{\partial \theta})
+\frac{R}{r^2\sin^2 \theta }\frac{\partial^2 Y}{\partial \varphi^2}=0
$$
移项、化简可得
$$
\frac{1}{R}\frac{\mathrm{d}}{\mathrm{d} r}(r^2\frac{\mathrm{d} R}{\mathrm{d} r})
=-\frac{1}{\sin \theta Y}\frac{\partial}{\partial \theta}(\sin \theta \frac{\partial Y}{\partial \theta})
-\frac{1}{Y}\frac{1}{\sin^2 \theta }\frac{\partial^2 Y}{\partial \varphi^2}
$$
我们发现,这个方程左边是与$R$有关的函数,右边是与$\theta,\varphi$有关的函数,显然两者不可能相等,除非他们同时等于一个常数
我们令这个常数为$l(l+1)$,于是得到两个方程
$$
\frac{\mathrm{d}}{\mathrm{d} r}(r^2\frac{\mathrm{d} R}{\mathrm{d} r})-l(l+1)R=0
$$
$$
\frac{1}{\sin \theta }\frac{\partial}{\partial \theta}(\sin \theta \frac{\partial Y}{\partial \theta})
+\frac{1}{\sin^2 \theta }\frac{\partial^2 Y}{\partial \varphi^2}
+l(l+1)Y=0
$$
第二个方程叫做球函数方程
如果我们进一步分离变量,令
$$
Y(\theta,\varphi)=\Theta(\theta)\Phi(\varphi)
$$
带入球函数方程,化简得到两个常微分方程
$$
\Phi’'+\lambda \Phi=0
$$
$$
\sin \theta \frac{\mathrm{d}}{\mathrm{d} \theta}(\sin \theta \frac{\mathrm{d \Theta}}{\mathrm{d} \theta})+[l(l+1)\sin^2\theta-\lambda]\Theta=0
$$
连带勒让德方程
上一步我们得到了两个常微分方程,第一个方程和自然周期条件构成本征值问题,在经过很多步的推导化简(感觉这些内容对我来说有些超纲),可以把第二个式子改写为
$$
(1-x^2)\frac{\mathrm{d}^2\Theta}{\mathrm{d}x^2}-2x\frac{\mathrm{d}\Theta}{\mathrm{d}x}+[l(l+1)-\frac{m^2}{1-x^2}]\Theta=0
$$
这个式子被称为$l$阶连带勒让德方程
这个式子的解,即函数$\Theta$的表达式为连带勒让德函数
级数解法
用球坐标系对拉普拉斯方程进行分离变数,得到了连带勒让德方程等特殊的函数方程,这些方程大多都是线性二阶常微分方程,很难用常规办法解,但可以用级数解法解出
常点与奇点
对于一个复变函数的线性二阶常微分方程
$$
\frac{\mathrm{d}^2w}{\mathrm{d}z^2}+p(z)\frac{\mathrm{d}w}{\mathrm{d}z}+q(z)w=0
$$
若系数函数$p(z)$、$q(z)$在点$z_0$的邻域中是解析的,则点$z_0$叫做该方程的常点,若点$z_0$是奇点,则点$z_0$叫做该方程的奇点



