Nabla算子
$\nabla$:Nabla算子,将数量场变成向量场
-
当其作用于函数,如$\nabla F(x)$,意思为求该函数梯度
-
当其点乘函数,如$\nabla \cdot F(x)$,意思为求该函数的散度
-
当其叉乘(三维)函数,如$\nabla \times F(x)$,意思为求该函数的旋度
函数可视化
对于函数$f(x,y)=x^2+y^2$,我们有两种可视化方法,第一种叫做图像:
$$
{(\vec{x}, f(\vec{x}))|\vec{x} \in D}
$$
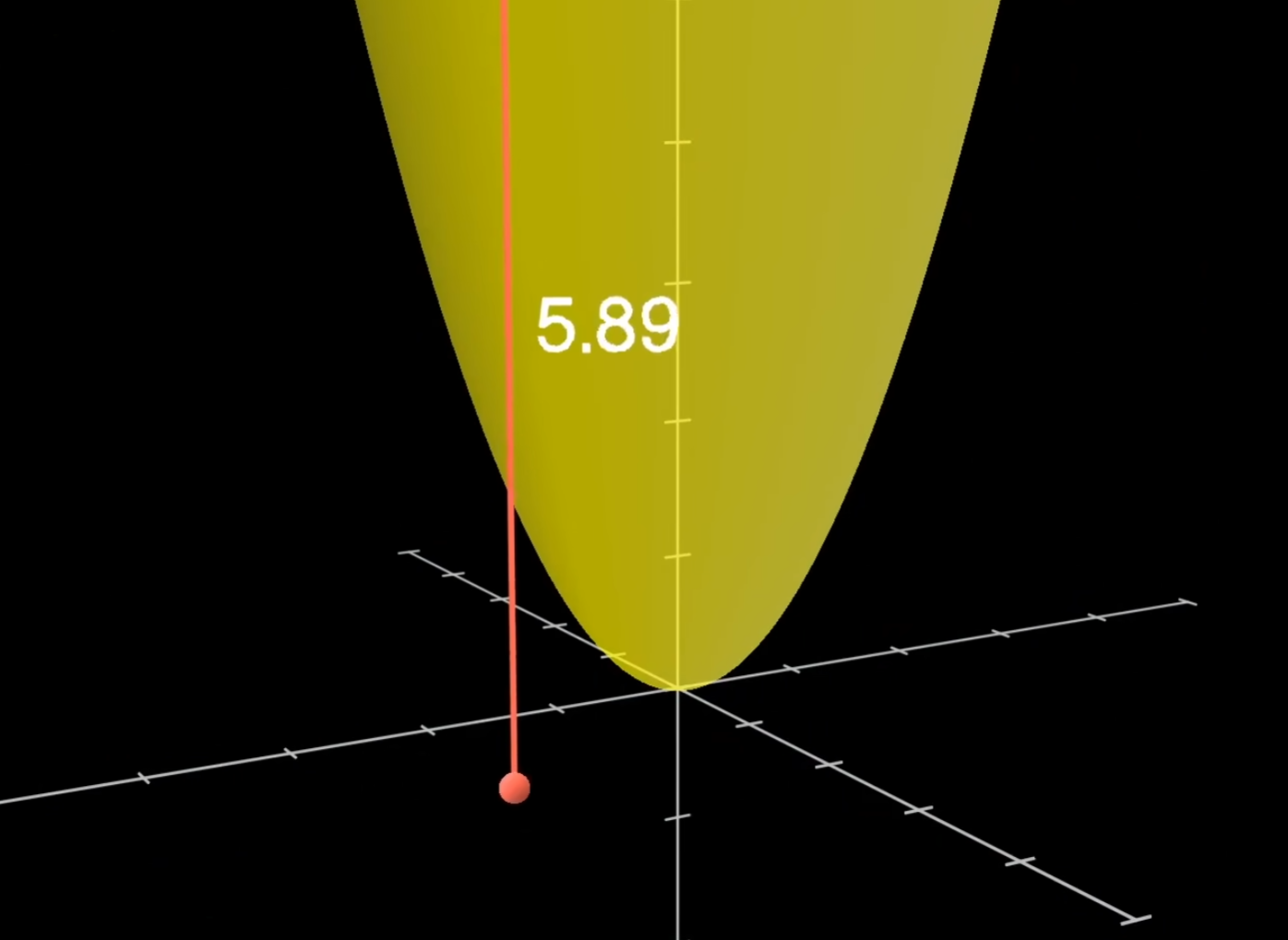
第二种叫做等值面:
$$
{\vec{x}|f(\vec{x})=c}
$$
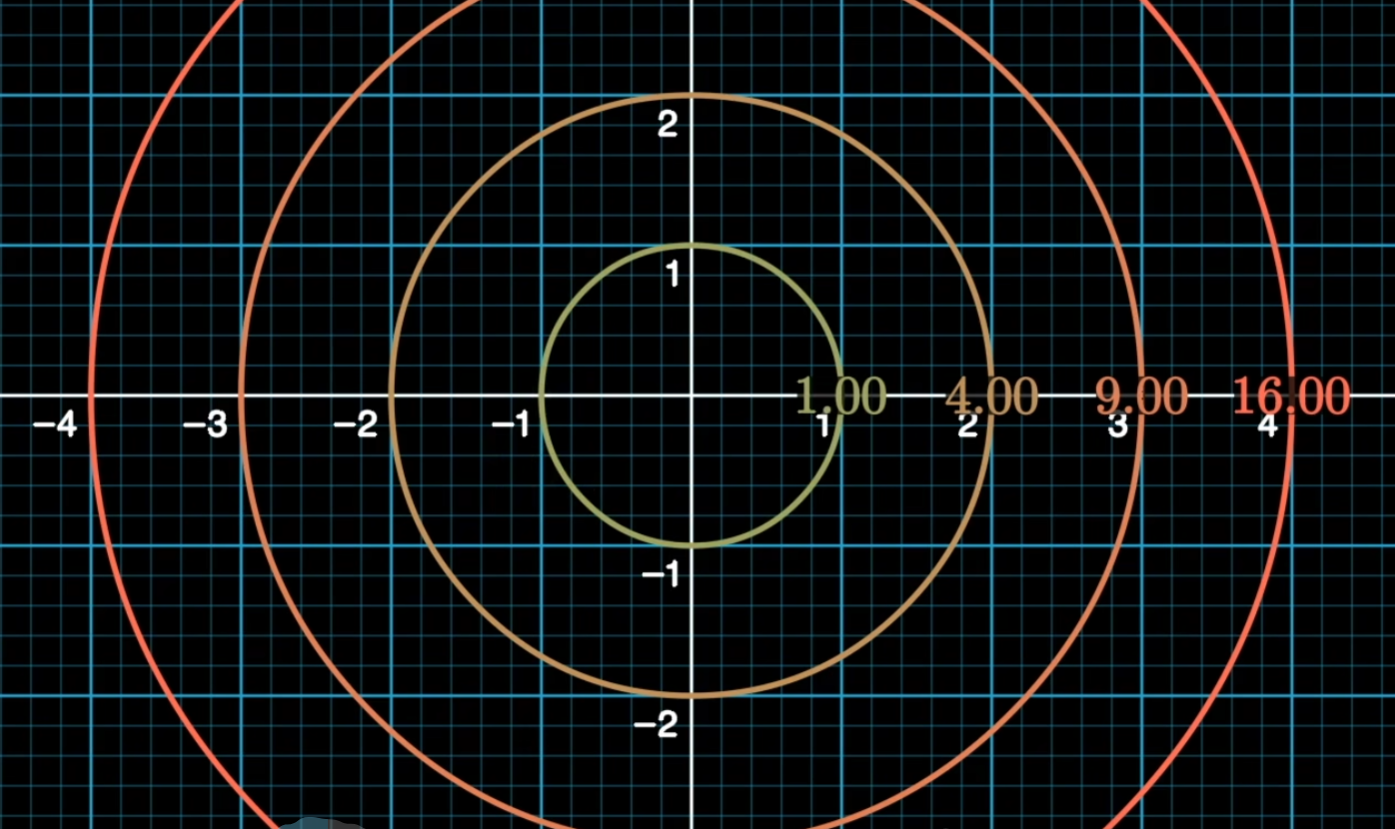
等值面只需要二维空间就能表示三维数据
梯度
Nabla算子其实是一个向量:
$$
\nabla =\left[
\frac{\partial }{\partial x_1}, \frac{\partial }{\partial x_2 },\cdots,\frac{\partial }{\partial x_n }
\right]^{T}
$$
Nabla算子作用于函数(标量场),可以将标量场转化为向量场,我们称该向量场为梯度
$$
\nabla f=
\left[
\begin{array}{c}
\frac{\partial f}{\partial x_1}\\
\frac{\partial f}{\partial x_2}\\
\vdots\\
\frac{\partial f}{\partial x_n}\\
\end{array}
\right]
$$
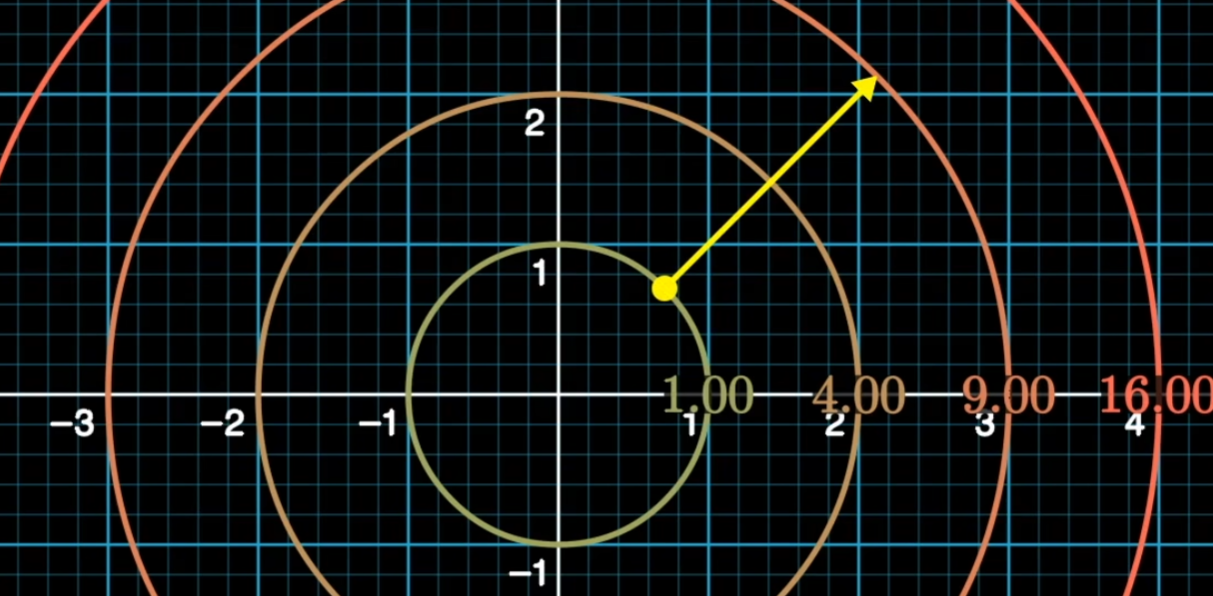
梯度垂直于等值面,意义为变化最快的方向(图中黄色箭头)
散度
我们知道向量和向量间可以进行点乘,其结果为一个标量,那么Nabla算子和向量相乘,我们称所得到的标量为散度
$$
\vec{f}=\left[
\begin{array}{c}
f_1\\
f_2\\
\vdots\\
f_n\\
\end{array}
\right]
$$
$$
\nabla \cdot \vec{f}=\frac{\partial f_1}{\partial x_1}+\frac{\partial f_2}{\partial x_2}+\cdots +\frac{\partial f_n}{\partial x_n}
$$
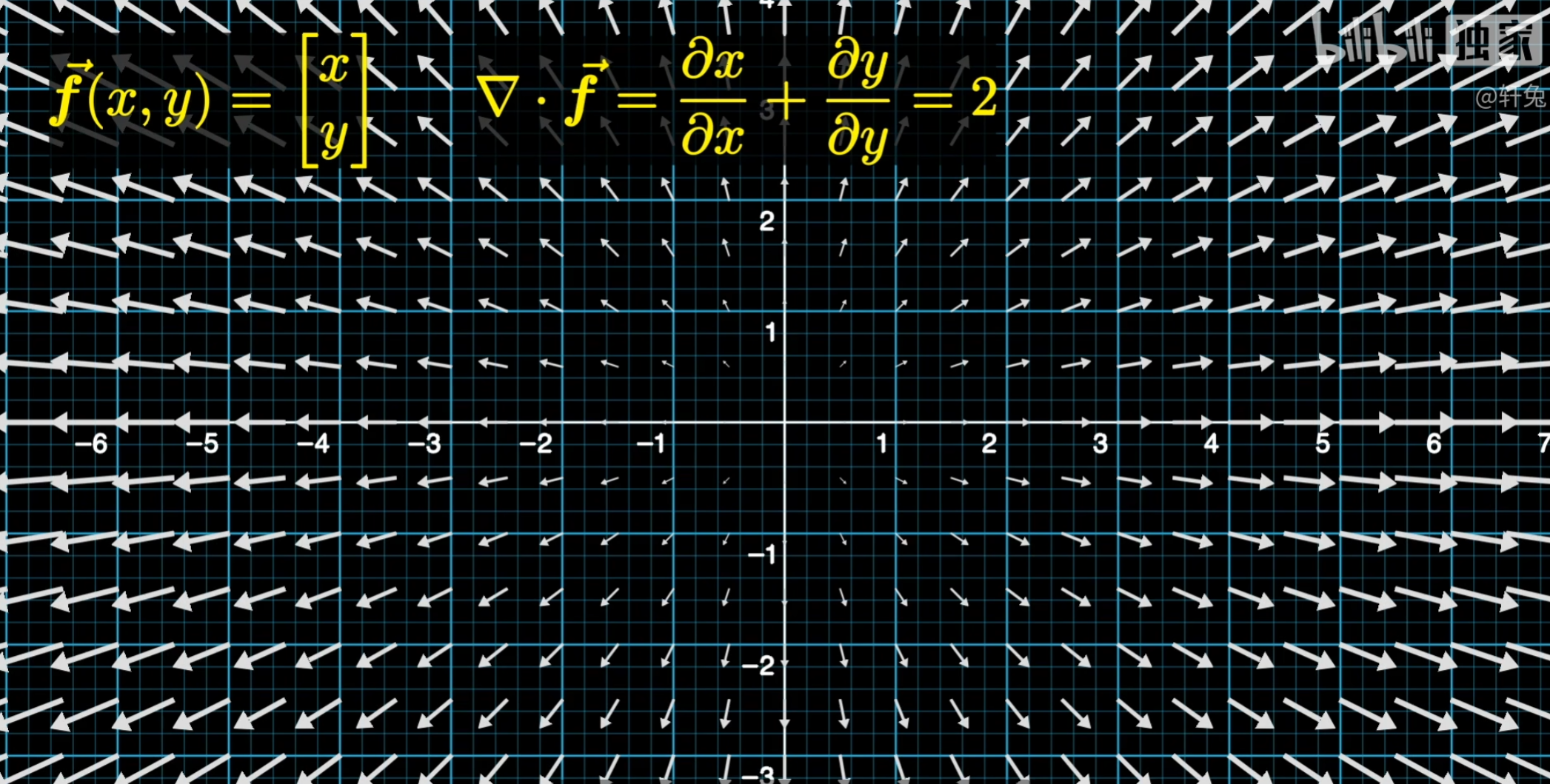
上图的白色箭头表示一个向量,我们发现这些箭头都是在朝外扩散,而散度就是用来衡量箭头向外扩散的程度
散度的物理意义是通量的局部描述。我们在图上画一个圈,我们发现会有向量进入这个圈,也有向量离开这个圈,那么进出之合,我们就称之为通量(比如磁通量),我们将通量除以圈的面积,就得到了通量的体密度。若这个圆取无穷小,那么体密度的极限值就是该点的散度
是不是突然很好理解麦克斯韦方程中$\nabla \cdot \mathbf{E}=0$的原因了?

其实这个公式就是高斯公式

旋度
向量不仅可以点乘,其实也可以叉乘,两个三维向量叉乘,能得到一个3x3的行列式。最后得到一个矩阵,我们称为旋度
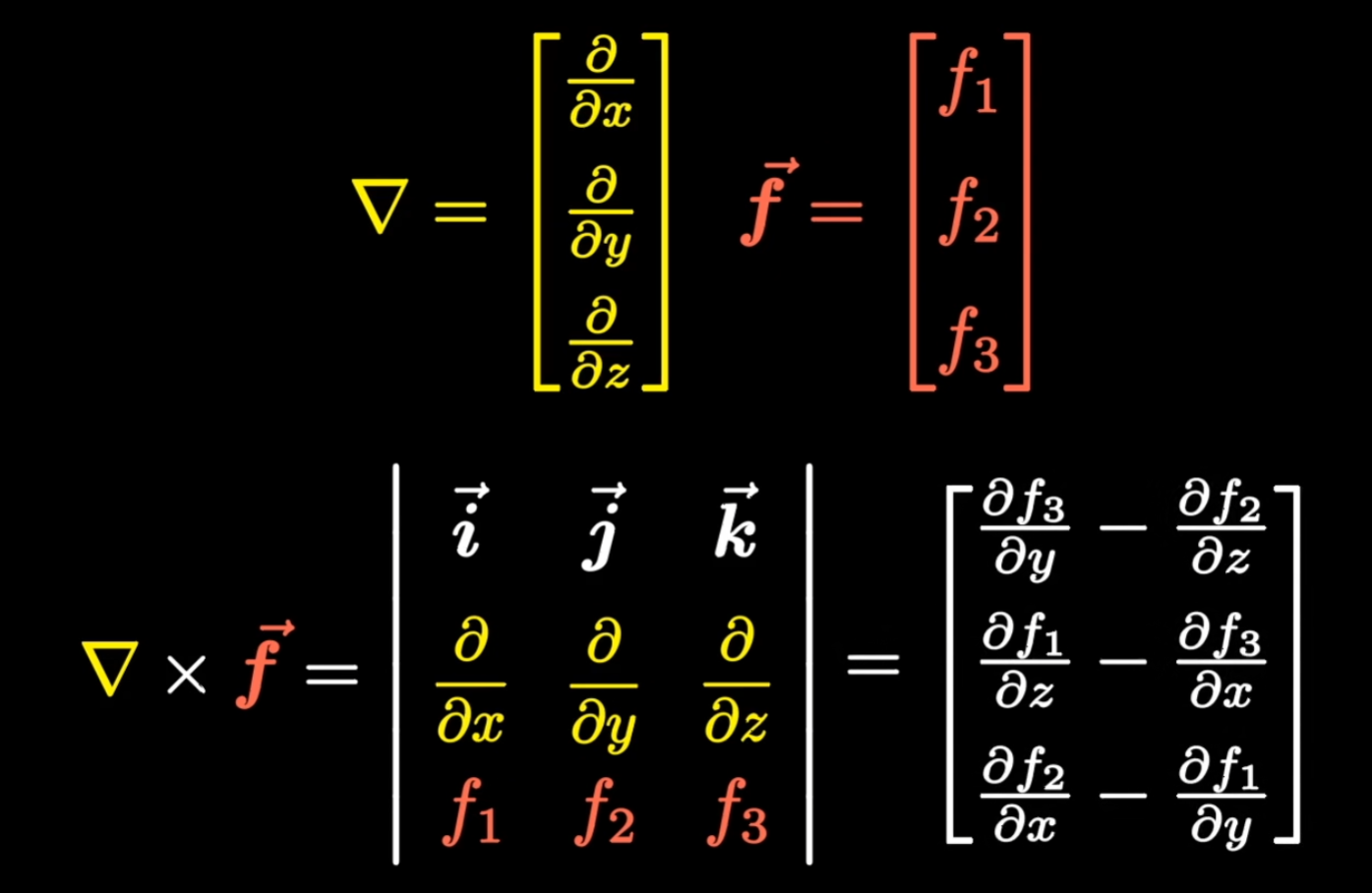
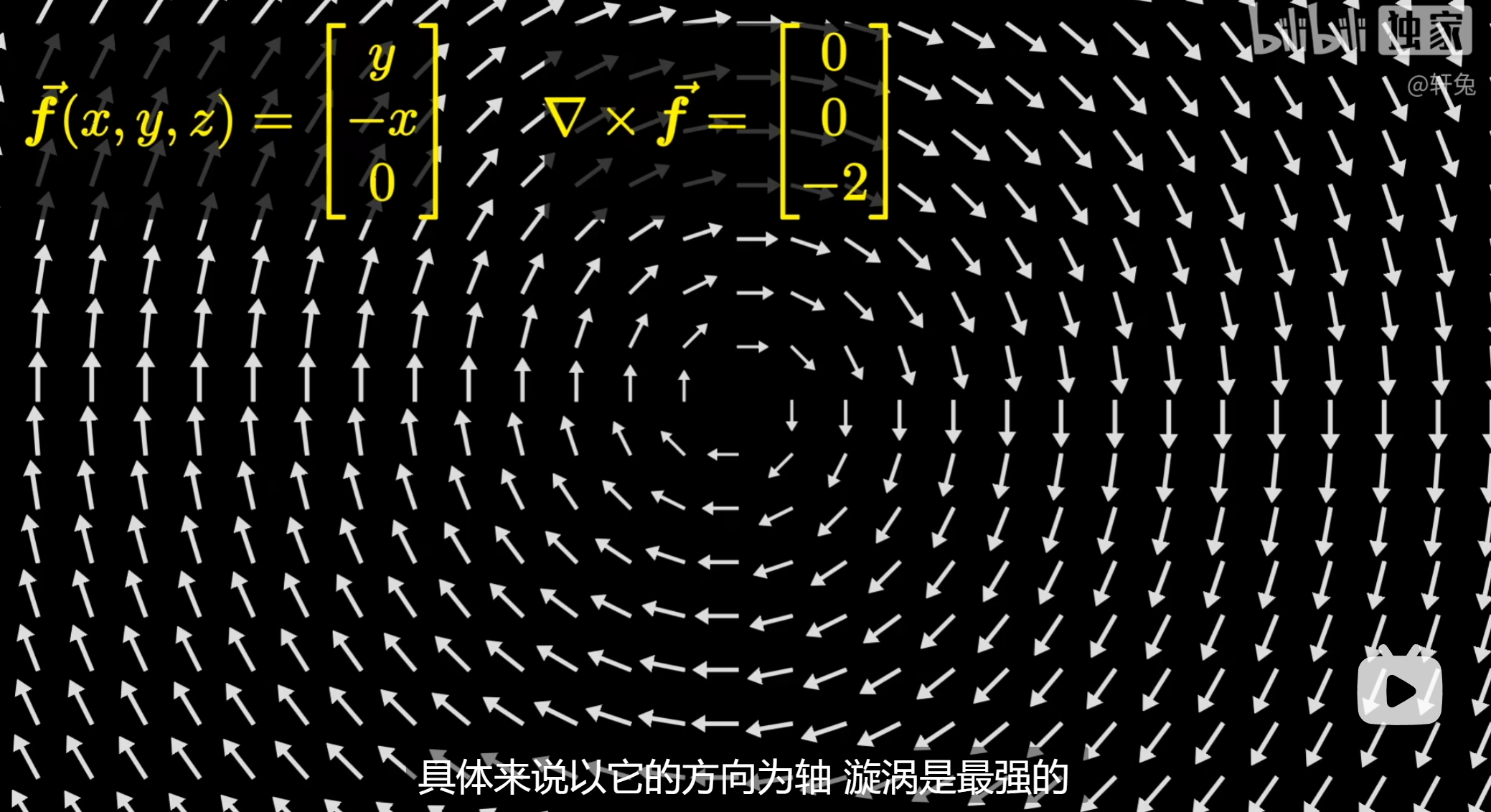
旋度的物理意义就是环量的面密度。现在有一个在旋转的场,我们在场上画一个圈,场在这个圈内会做功,这个功就是环量,我们求出单位面积上环量,这个极限值描述了漩涡的强度。旋度就是旋转最快的方向

梯度的散度
nabla算子和自己做内积,于是会得到一个数量场,意义为求梯度的散度
这个操作为$\nabla\cdot \nabla$,也可以写作$\nabla^2、\nabla^T \nabla$,但为了避免歧义,我们引入了一个新的符号,拉普拉斯算子
$$
\Delta=\nabla \cdot\nabla
$$



