插值
线性插值
$$
\mathrm{lerp}(p_0,p_1;t)=(1-t)p_0+tp_1
$$
Smoothstep
Hermite
将一个数平滑映射到[0, 1]
float v = smoothstep(0.0, 1.0, time);
|
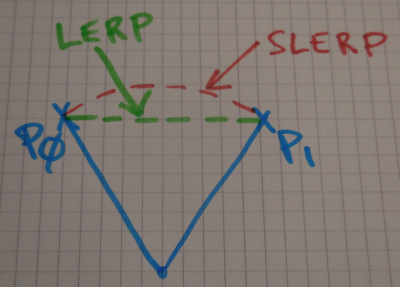
球面插值
Slerp
在球面上线性插值
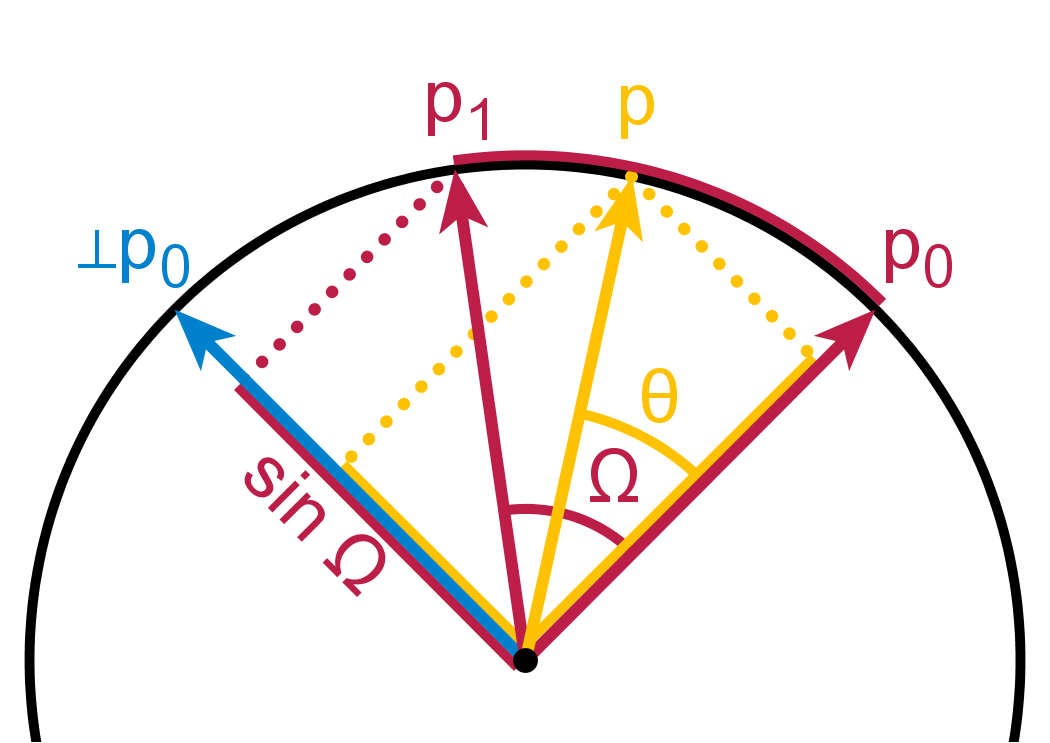
$$
\mathrm{Slerp(p_0,p_1;t)}=\frac{\sin[(1-t)\Omega]}{\sin \Omega}p_0+\frac{\sin [t\Omega]}{\sin \Omega}p_1
$$
vec4 Slerp(vec4 p0, vec4 p1, float t)
{
float dotp = dot(normalize(p0), normalize(p1));
if ((dotp > 0.9999) || (dotp<-0.9999))
{
if (t<=0.5)
return p0;
return p1;
}
float theta = acos(dotp * 3.14159/180.0);
vec4 P = ((p0*sin((1-t)*theta) + p1*sin(t*theta)) / sin(theta));
P.w = 1;
return P;
}
void main()
{
vec4 P = Slerp(gxl3d_Position, gxl3d_Attrib1, time);
gl_Position = gxl3d_ModelViewProjectionMatrix * P;
Vertex_Color = gxl3d_Attrib0;
}
|
参考
glsl-simple-morph-target-animation





