《Stochastic Screen Space Reflections》阅读笔记

2015年SIGRAPH，EA提出了SSSR，用于《镜之边缘》中镜面反射

需求有

支持清晰（sharp）和模糊（blurry）反射
邻接性，越近反射越清晰（contact hardening）
高光拉伸
逐像素的粗糙度和法线

作者的算法

将屏幕划分为Tile，进行一次低分辨率的光线步进，评估Tile的重要性，需要多少射线
根据材质粗糙度判断使用何种的RayMarching
- 昂贵的射线：借助Hi-Z的精确tracing，能得到准确的命中点
  - 用于smooth表面
- 便宜的射线：简单的线性步进
  - 用于粗糙表面（反正会做严重的滤波，不需要高精度）
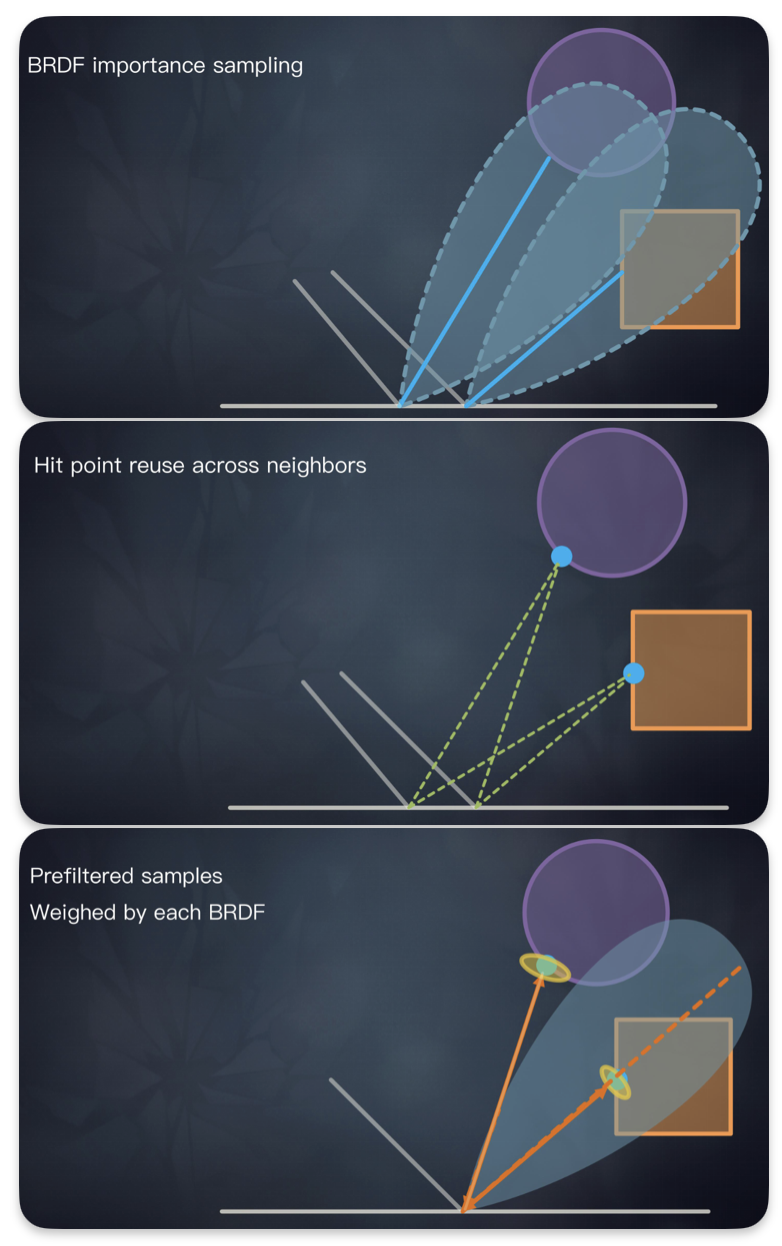
使用BRDF重要性采样决定射线方向
使用邻居的采样信息进行模糊
TAA

Tile评估

对于每一个Tile以1/8分辨率发射射线
判断射线（的反射光线）是否击中
1. 若所有光线都没命中，则跳过这个Tile的步进
2. 根据命中的比例和命中信息的差异，判断这个Tile中的像素需要多少个光线

Hi-Z tracing

详情可以去看《GPU Pro 5》

Hi-Z使用四叉树组织屏幕深度，将层次关系存储在MipMap层级中，用于加速反射光线的求交

Hi-Z的构建时，对屏幕尺寸的深度进行滤波，每次保存2x2像素中最浅的像素，也就是说最高级别的Hi-Z存储着整张图中最浅的深度

用C点表示光线在步进过程中的头坐标，我们射线求交的原理就是判断C点距离相机的距离和该点深度图的深度关系，相交处必然是一侧比C点深，一侧比C点浅

此外还有几条经验：

从相机出发的射线，落点位置是View空间该方向最浅的位置
从相机出发的射线，与落点位置的法线夹角应该大于$45^{\circ}$
- 若夹角小于$45^{\circ}$，那么反射信息来自相机身后的内容，屏幕空间没有这些信息（可以用Cubemap补充信息）
- 若夹角大于$45^{\circ}$，那么我们基本可以认为，反射光线在步进过程中，深度在不断变深
我们实际寻找的是，光线在步进过程中，比C点要深的最浅位置（更深，但只能深一点点）
由于起初我们位于最浅的位置，而步进的光线越来越深，因此第一个min-Z小于C点深度的位置，就是交点位置，我们只需要一直向右，不用回头
- 这样得到的Mip等级比较高，我们通过降低Mip等级，每次取比C深中最浅的那一个，直到Mip为0

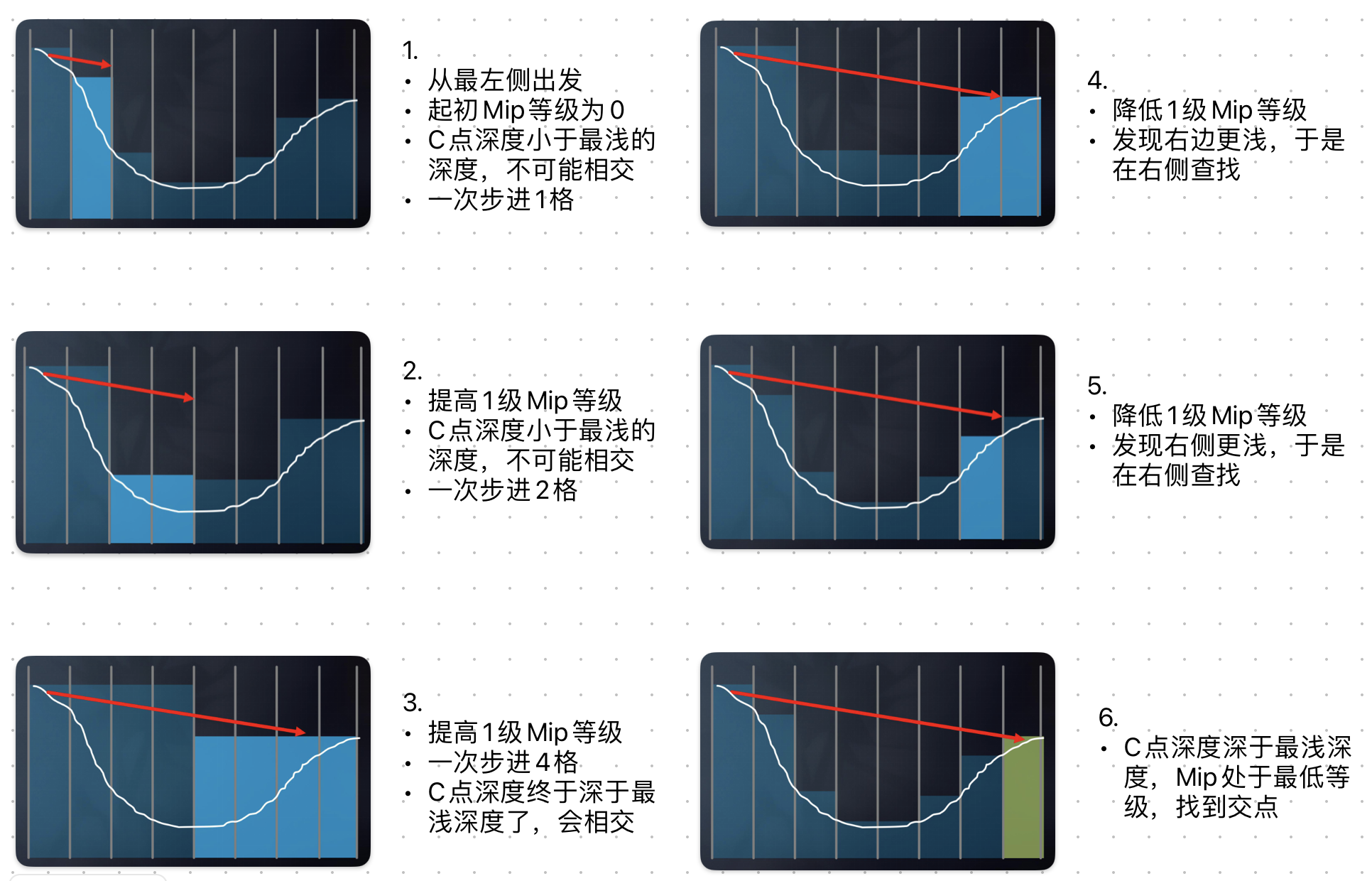
算法复杂度为$O(\log n)$

重要性采样

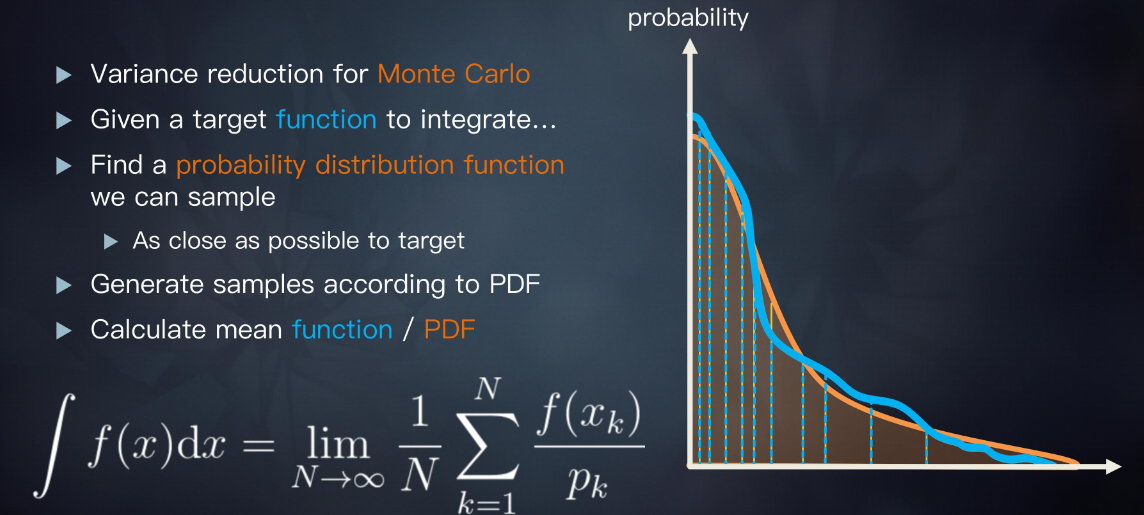
重要性采样是蒙特卡洛积分中用于减少方差的算法，详情可以去看PBRT

简单来说就是我们有一个积分，我们不得不实时求这个积分，于是我们将这个积分很多项分离出去，最后变成了复杂离散项 x 一段简单函数的积分

蒙特卡洛积分

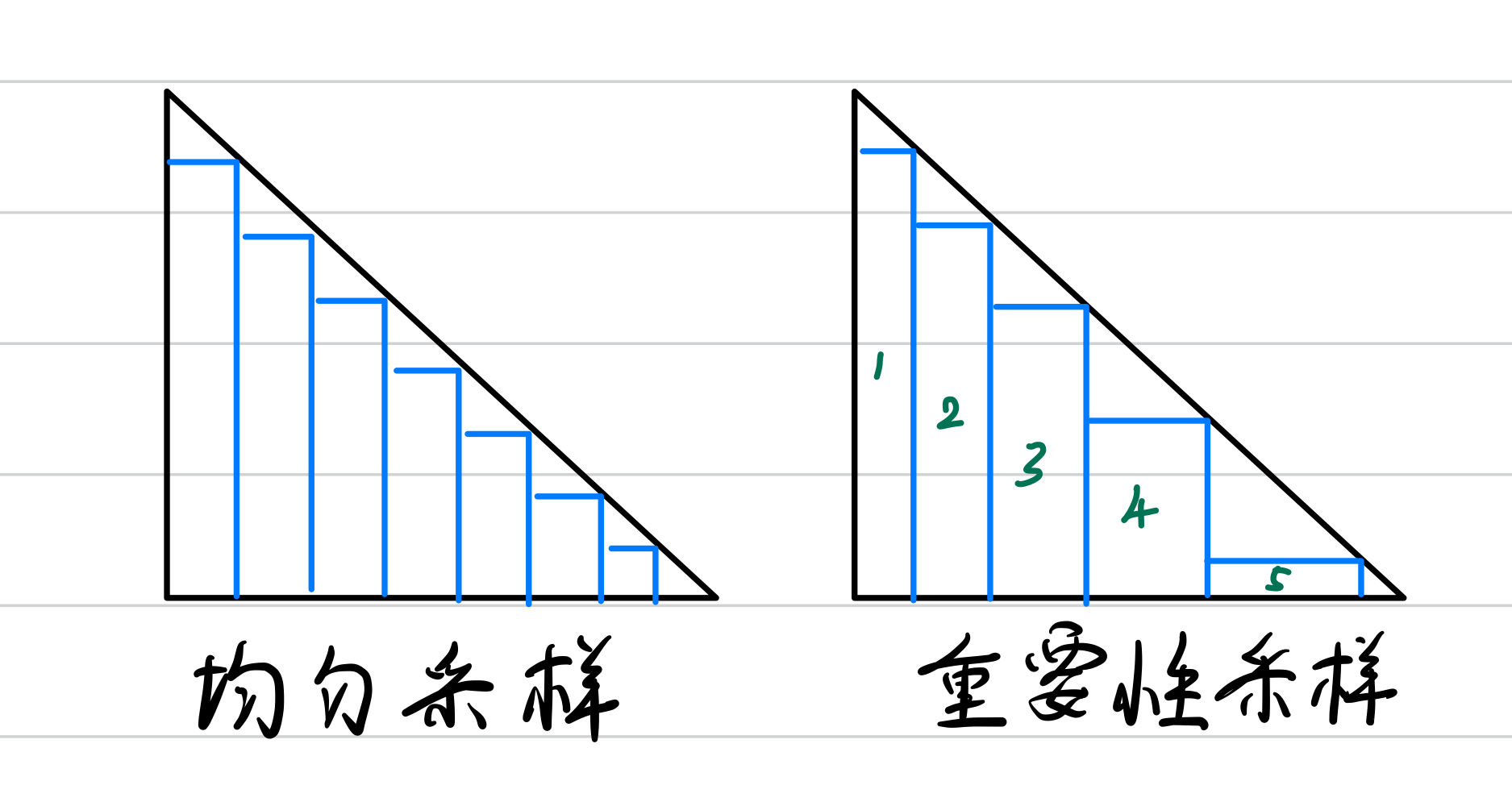
这是一个三角形，如果我们想求三角形的面积，可以对三角形的高度函数做积分

第一种切分方法：均匀切分，三角形被分为等宽的长方形，每个长方形长$\Delta x$，高$\sqrt{1-x^2}$

$$
S=\sum _{i=0}^N \Delta x \times h_i
$$

第二种切分方法：重要性切分，左侧长方形更窄，右侧更宽

$$
S=\sum _{i=0}^N x_i \times h_i
$$

三角形切被分为一个个长方形，长方形的面积代表贡献。很显然，左侧的长方形高度越高，相同宽度面积越大，贡献越多。也就是说，相同的x轴变化，左侧部分对积分的影响越明显，越高频

能看出（在同等误差下）重要性采样所需要的采样次数比均匀采样要小

重要性采样的思想就是，在高频处我们进行更多次的采样，低频处进行更少的采样，最后根据权重合并，就能在采样次数比较少的情况下，得到最精确的积分值

高度函数$h_i$就是采样值
宽度函数$x_i$就是重要性权重
面积$S$就是在当前概率分布下的采样期望

概率密度函数

详情可以去看概率论

在上一步，我们将连续函数的积分，转化为离散的采样值 x 重要性权重，然后我们发现，这个重要性权重怎么求？

还是上面的三角形，我们发现横坐标可以取[0, r]中任意值（r为三角形边长）

因此具体到某个点（随机变量），被取到的概率为$\frac{\mathrm{d}x}{r}$（这里其实不怎么精确，概率论中点取到的概率为0，这里实际上是一段很小的区域被取到的概率）

对于一个区域[a, b]，我们进行积分，得到随机变量取到该区域的概率P
$$
P(a < X \le b)=F(b)-F(a)=\int_a^b \frac{1}{r}\mathrm{d}x=\frac{b-a}{r}
$$

分布函数：$F(x)$
概率密度函数：$1/r$，我们用$p(x)$表示
概率：$P(a < X \le b)$

哦，现在我们知道了这个重要性权重有多大了
$$
x_i=\Delta x/P=1/p(x)
$$
进而我们可以写出这个三角形面积的期望
$$
S=\sum _{i=0}^N x_i \times h_i=\lim {N \rightarrow \infty}\frac{1}{N}\sum{k=1}^{N}\frac{f(x_k)}{p(x)}
$$

不过，值得注意的是，我们上面使用的PDF是均匀的，其实并能很好地加速收敛，实际会使用一个和原函数形状类似的PDF来加速收敛（PDF的选择不会影响最终结果，但是会影响收敛速度）

BRDF生成射线方向

BRDF，双向反射分布函数，用于描述光线进出材质后能量的变化

我们在实现BRDF时，通常会实现以下接口

eval：给定入射光方向和视线方向，求BRDF值
sample：生成射线方向
pdf：返回sample生成的射线的PDF

我们以最简单的phong着色为例

在RTOW中，我们朝着随机半球方向生成向量，该向量就是新射线的方向，同时求出该方向的PDF

我个人理解，射线方向是随机生成的，每个方向出现的可能性相同，但是他们的PDF不同，你可以理解为重要性采样求三角形面积时，每个大长方形是由内部多个（数量相同）等高的小长方形拼成的，但是小长方形的宽度不一致，1/PDF就是小长方形的宽度。越重要的地方，长方形宽度越小，越密集，于是实现了重要性采样

virtual bool scatter(
        const ray& r_in, const hit_record& rec, color& alb, ray& scattered, double& pdf) const override {
            auto scatter_direction = rec.normal + random_unit_vector();
            // Catch degenerate scatter direction
            if (scatter_direction.near_zero())
                scatter_direction = rec.normal;
            scattered = ray(rec.p, unit_vector(scatter_direction), r_in.time());
            alb = albedo->value(rec.u, rec.v, rec.p);
            pdf = dot(rec.normal, scattered.direction()) / pi;
            return true;
        }

上面生成新射线方向时，使用法线+球面向量，最后的形状就类似下图红色

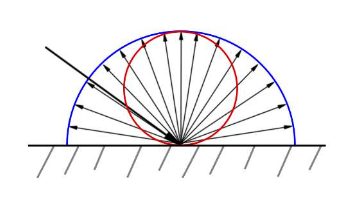
还清除了朝下（射向材质内部的）的射线

随机数

作者使用了Halton Sequences生成随机数，并引入了截断，角度有最大值，这样能减弱BRDF的长尾巴（Tail）对结果的影响（这些尾巴会带来很多噪点）

float2 u = halton(sampleIdx);
u.x = lerp(u.x, 1.0, bias);
importanceSample(u);

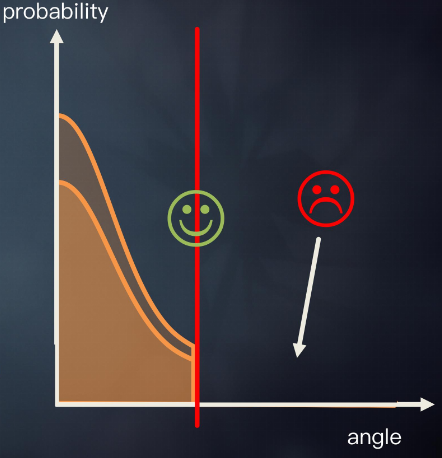
过滤重要性采样

一种基于预计算的光追，我们假设射线是圆锥形，我们可以根据MipMap层级得到滤波结果

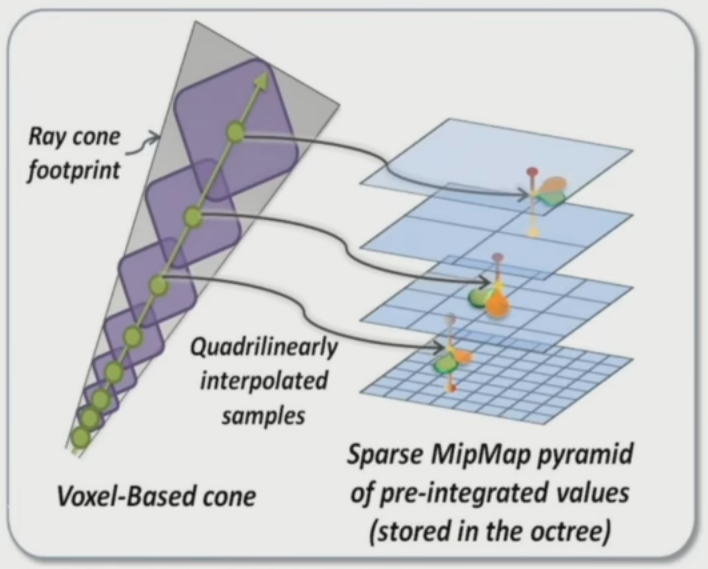
复用邻居光线

复用

上面提到glossy ssr会导致严重的噪点问题，即使使用重要性采样，每个像素仍需要大量光线才能得到低噪点的结果

我们注意到，相邻像素，他们的位置相近，可见性应该也是接近的，那么邻居像素朝某方向发射的光线，其实也可以被当前像素复用

当然直接做模糊（比如用高斯滤波）会导致很多光斑，经过很多数学推导和近似后，给出了以下公式

result = 0.0;
weightSum = 0.0;
for(auto& pixel : neighborhood){
    weight = localBRDF(pixel.hit) / pixel.hitPDF;
    result += color(pixel.hit) * weight;
    weightSum += weight;
}
result /= weightSum;

稀疏

受邻居光线的启发，我们完全没必要每个像素都做射线，只需要在低分辨率下某些点做多次射线，其邻居使用这个射线结果就可以

TAA

我们不仅在空间上做射线的复用，也可以在时间上及逆行复用

参考

SSR

SSSR

《Stochastic Screen Space Reflections》阅读笔记

相关工作

mirror-only SSR

glossy SSR

模糊滤波

重要性采样

作者的算法

Tile评估

Hi-Z tracing

重要性采样

蒙特卡洛积分

概率密度函数

BRDF生成射线方向

随机数

过滤重要性采样

复用邻居光线

复用

稀疏

TAA

参考