抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

Reuben Sun

主页

图形

引擎

AI

编程

数学

光学

DCC

游戏

垃圾回收

engine

发布于：2023年1月31日

垃圾回收

前言

《垃圾回收的算法与实现》读书笔记，其中的代码大多为伪代码

一：概念

GC，Garbage Collection，垃圾回收

功能

  • 找到内存中的垃圾
  • 回收垃圾

为什么需要GC

如果没有GC，程序员需要手动进行内存管理，开发麻烦，容易引发内存泄漏、野指针，而且因此导致的BUG很难被定位，修复麻烦

如果有GC，就可以避免这些问题

GC的种类

  • 保守式GC：不能识别指针和非指针时，一律视为非指针
  • 准确式GC

GC的算法

  • 标记清除法：标记活动对象，其他的都回收
  • 引用计数法：回收引用值为0的对象
  • GC复制法：复制活动对象，其他的都回收

GC的选取

  • 最大暂停时间短：游戏
  • 整体处理时间短：音频编码

对象

这里的对象并不是OOP里的Object，而是被应用程序使用的数据的集合，对象由头和域构成

  • 头（header）：包含对象的大小和种类

  • 域（field）：参考OOP里的成员

对象分为活动对象和非活动对象，GC会保留活动对象，销毁非活动对象

mutator

可以简单理解为应用程序，在程序运行过程中，会分配/调用/改变对象（只能操作活动对象），伴随着mutator运行，会产生垃圾

GC算法的评估标准

  • 吞吐量（throughput）：单位时间的处理能力
  • 最大暂停时间（在进行GC时，mutator会被暂停）
  • 堆使用效率
  • 访问局部性

二：标记清除法

学这一节之前想想操作系统里文件系统

该算法分为两步

  1. 标记阶段：将所有活动对象做上标记
  2. 清除阶段：将所有没被标记的对象回收

标记阶段

  1. 通过根，找到直接引用的对象，标记
  2. 递归标记所有能访问到的对象（常用深搜，因为内存使用量更少）
void mark(obj){
	if(!obj.mark) 
        obj.mark = true;
	for(child: obj.children) 
        mark(*child);
}

清除阶段

遍历堆，回收所有没有被标记的对象，并将其放入空闲链表，以备分配

分配策略

在创建新对象obj时，遍历空闲链表，寻找合适的块，这里使用First-fit算法（因为快）

  • First-fit：找到第一个能放下obj的块
  • Best-fit：找到最小的能放下obj的块
  • Worst-fit：找到最大的能放下obj的块

合并策略

分配和回收会导致大量小的分块，于是需要合并，在这里直接遍历堆，将连续的空闲块合并

评价

优点

  • 实现简单
  • 与保守式GC兼容（因为对象不会被移动）

缺点

  • 碎片化，导致空间浪费，访问性能降低
  • 不支持写时复制（比如UNIX中的fork()）

优化方案

分级空闲链表

使用多个空闲链表，分别只连接不同大小的分块，分配时先找所对应的区间，可以提高性能

BiBOP（Big Bag Of Pages）

将大小相近的对象整理成固定大小的块进行管理

  • 碎片化的原因之一是杂乱散布的大小各异的对象，如果将堆固定分割，就可以减缓碎片化
位图标记

不直接堆对象进行标记，而是记录对象的标志位，存储在一个表格中

  • 与写时复制技术兼容（因为不会修改对象本身，可以复用）
  • 清除标志位更高效（只需要把表中要清除的对象的标志位改成一个特殊值）
延迟标记清除法
  • 分配时，先调用清除，如果能清出足够的空间来分配，则直接分配，否则进行普通的标记操作
  • 清除时，同样是First-fit遍历堆，但遍历的起点是上次开始的地点的右侧
  • 延迟的内核是不主动清除，而是等到要分配时再清除

三：引用计数法

学这一节前，想想智能指针

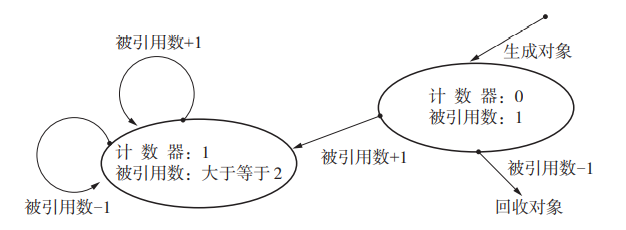
引用计数法中，对象会记录自己被引用次数，主要分为两个阶段

  1. 创建新对象：分配内存，将对象引用次数设为1
  2. 更新指针：先增后减计数器值，若引用次数为0则回收
//更新指针ptr，让其指向obj
void update_ptr(ptr, obj){	
	inc_ref_cnt(obj);	//obj要被ptr引用了，所以obj计数值++
    dec_ref_cnt(*ptr);	//ptr之前引用的东西不再被引用
    *ptr = obj;
}
void dec_ref_cnt(obj){
    obj.ref_cnt--;	//obj不再被引用，所以计数值--
    if(obj.ref_cnt == 0){	//如果obj没人用了，obj就要被清除
        for(child: obj.children){	//obj被清除了，那obj引用的对象，被引用次数要--
            dec_ref_cnt(*child);
        }
        reclaim(obj);	//执行回收
    }
}

评价

优点：

  • 对象变成垃圾时立刻被回收（延迟标记清除算法要等到分块用尽后才开始回收垃圾）
  • 最大暂停时间短（只有在更新指针的时候才会打断mutator）
  • 减少延根指针遍历所有子节点的次数（尤其在分布式系统中，效果显著）

缺点

  • 频繁进行计数值的操作
  • 计数器本身空间比较大（32位系统的计数器就要32位大小）
  • 循环引用无法回收
    • 如果两个物体互相引用，并不和其他对象有联系，于是他们成为了一座“孤岛”，成为了事实意义上的垃圾，但是却无法被回收（因为只要被引用，就不算垃圾）

优化方案

延迟引用计数法

解决频繁操作

  • 使用ZCT表（Zero Count Table），记录所有执行dec_ref_cnt后计数值变成0的对象（也就是说计数值变成0，不会立刻被视为垃圾回收），当ZCT表满了以后，开始回收表中的对象
  • 优点：延迟了根引用的计数（只有要回收时才会一起操作），降低了计数值的操作频率
  • 缺点
    • 不再能即刻回收垃圾（你可以理解为以前有垃圾就仍，现在要先堆一波垃圾再扔）
    • 最大暂停时间延长（scan_zct()要访问整个ZCT，这个过程muator是被中断的）
void dec_ref_cnt(obj){
    obj.ref_cnt--;
    if(obj.ref_cnt == 0){	//计数值变为0，可能会变成垃圾
        if(is_full($zct)){
            scan_zct();		//如果zct表满了，就扫描zct，并回收
        }
        push($zct, obj);	//将obj放入zct表
    }
}
void scane_zct(){
    fot(r: $root){
        (*r).ref_cnt++;	//根直接引用的对象的计数器++，直接引用计数时，根会极频繁改动
    }
    for(obj: $zct){
        if(obj.ref_cnt == 0){
            remove($zct, obj);
            delete(obj);
        }
    }
    fot(r: $root){
        (*r).ref_cnt--;	
    }
}
Sticky引用计数法

解决空间浪费

32位电脑意味着可以有$2^{32}$个对象，这些对象可能都会引用obj，所以obj的计数位应当可以记录被引用$2^{32}$次，所以计数位要有32位

如果计数位太少，一些比较大的对象就无法正常表示（直接做饱和运算，汽车速度超过速度计的最大值会停在最大值处），一旦出现这种情况，我们可以

  • 什么都不做
    • 这会导致如果一个物体被引用的次数特别多，超出了目前表示的范围，即使他变成了垃圾也无法回收
    • 但是，事实上绝大多数对象计数值一直在0和1间变化（生成后立刻回收），所以很少出现溢出
    • 而且一个对象被频繁引用，说明他十分重要，十分重要的东西被回收的概率并不大
    • 很多时候不需要保证内存永不泄露，只需要保证一段时间内不泄露就行，很多软件，用户不会一直开着的
  • 结合使用标记清除算法
    • 什么都不做，可能会导致内存耗尽，如果耗尽，那就用标记清除法清一次（相当于垃圾太多了，管不来了，就干脆来一次大扫除）
//标记
void mark(){	
    for(r: $roots){
        push(*r, $stack);	//将所有根直接引用对象入栈
    }
    while(!$stack.empty()){
        obj = pop($stack);
        obj.ref_cnt++;
        if(obj.ref_cnt == 1){	//这说明obj只进栈一次
            for(child: obj.children){
                push(*child, $stack);
            }
        }
    }
}
//清除
void sweep(){
    index = $heap_top;
    while(index < $heap_end){	//遍历整个堆
        if(index.ref_cnt == 0){
            reclaim(index);		//回收计数值为0的对象
        }
        index += index.size;
    }
}
一位引用计数法

是Sticky的极端，计数位只有一位（两个tag，一个MULTIPLE，一个UNIQUE），而且将计数位放在指针上，而非放在对象上

一位引用计数

void copy_ptr(dest_ptr, src_ptr){
    delete_ptr(dest_ptr);
    *dest_ptr = *src_ptr;
    set_tag(dest_ptr, MULTIPLE);
    if(src_ptr.tag == UNIQUE){
        set_tag(src_ptr, MULTIPLE);
    }
}
void delete_ptr(ptr){
    if(ptr.tag == UNIQUE)	
        reclaim(*ptr);	//如果对象以前只被引用一次，那么这次就要被回收
}

优点

  • cache命中率高

缺点

  • 同Sticky，而且更严重
部分标记清除法

解决循环引用

只对可能会有循环引用的对象使用标记清除法，其他对象使用引用计数法

每个对象会有两个状态位（于是就有四个状态），分别为

  • BLACK：绝对不是垃圾的对象（初始值）
  • WHILE：绝对是垃圾的对象
  • GRAY：搜索完毕的对象
  • HATCH：可能是循环垃圾的对象
void dec_ref_cnt(obj){
    obj.ref_cnt--;
    if(obj.ref_cnt == 0){
        delete(obj);
    }
    else if(obj.color != HATCH){
        obj.color = HATCH;
        queue.push(obj);
    }
}

对放入队列的对象进行标记清除算法

Object new_obj(size){
    obj = pickup_chunk(size);	//分配内存
    if(obj != null){	//如果分配成功
        obj.color = BLACK;
        obj.ref_cnt = 1;
        return obj;
    }
    else if(!queue.empty()){	//说明现在空间不足，要回收垃圾，先看是否存在HATCH物体
        scan_hatch_queue();		
        return new_obj(size);	//回收queue内后重新尝试分配
    }
    else{
        allocation_fall();
    }
}
void scan_hatch_queue(){	//循环扫描队列，直至队列为空
    obj = queue.pop();
    if(obj.color == HATCH){
        paint_gray(obj);	//把obj和其孩子变为GRAY，孩子们引用值--
        scan_gray(obj);		//引用值>0涂黑，等于0涂白
        collect_while(obj);
    }
    else if(!queue.empty()){
        scane_hatch_queue();
    }
}
void paint_gray(obj){
    if(obj.color == (BLACK | HATCH)){	
        obj.color = GRAY;	
        for(child: obj.children){
            (*child).ref_cnt--;
            paint_gray(*child);
        }
    }
}
void scan_gray(obj){
    if(obj.color == GRAY){
        if(obj.ref_cnt > 0){
            paint_black(obj);
        }
        else{
            obj.color = WHITE;
            for(child: children(obj)){
                scan_gray(*child);
            }
        }
    }
}
void paint_black(obj){
     obj.color = BLACK;
	 for(child : children(obj)){
		(*child).ref_cnt++
		if((*child).color != BLACK){
			paint_black(*child)            
        }          
     }		
}
void collect_while(){
    if(obj.color == WHILE){
        obj.color = BLACK;
        for(child: obj.children){
            collect_while(*child);
        }
        reclaim(obj);
    }
}

优点

  • 可以回收循环引用

缺点

  • 一个对象要被查找三次，导致最大暂停时间+++

四：GC复制法

想一下渲染中的双缓冲

先把整个空间分为等大的两部分，From和To，我们用From空间分配活动对象

GC时，把所有活动对象（递归）复制到其他空间（To空间），然后把原空间（From空间）所有对象回收，然后把空间互换

评价

优点

  • 吞吐量大
  • 分配速度快（Frist-fit）
  • 不会发生碎片化（每次回收时，都会把所有对象重新排在From空间的开头，这个操作被称为压缩）
  • 兼容缓存

缺点

  • 堆效率低（因为二等分后，只能利用其中一半）
  • 不兼容保守式GC
  • 复制对象时要递归复制，会消耗栈，可能导致栈溢出

优化方案

Cheney GC复制法

从递归复制改为迭代复制（基于队列的广度优先搜索）

下图搜索顺序：A BC DEFG HIJKLMNO

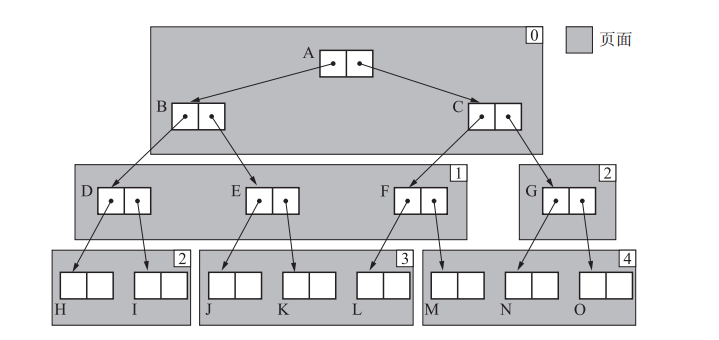
![Cheney GC](/images/Cheney GC.png)

优点

  • 从递归变成迭代，降低栈压力

缺点

  • 不利于缓存（在上图，我们假设每个页最多存放三个块，我们发现有引用关系的对象很可能不在同一个块中）
近似深度优先搜索方法

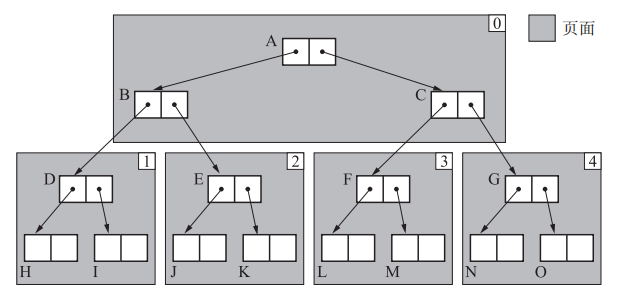
在页间做深度优先搜索，在页内做广度优先搜索

下图搜索顺序：ABC DHI EJK FLM GNO

近似深度优先

多空间复制法

把空间分成十份，一个From，一个To，八个标记清除法

五：标记压缩法

结合了标记清除法的标记+GC复制法的压缩

Lisp2算法

类比原地删除数组中某个元素

标记方法和标记清除法一样，标记后遍历堆，将所有活动对象压缩到左侧

Lisp2标记

Lisp2压缩

Lisp2结束

优点

  • 比GC复制法堆效率高，比标记压缩法碎片少

缺点

  • 三次遍历堆，效率过低

Two-Finger算法

这个算法优缺点很明显，所以先说优缺点，再谈实现

优点

  • 只需要两次遍历堆
  • 不需要额外的forward指针（Lisp2的对号）

缺点

  • 对象大小必须一致（可以与BiBOP结合使用）
  • 压缩时破坏排序（一般有引用关系的对象会放在一起），于是不适合缓存

在Lisp2算法中，可以说几乎每一个活动对象都需要移动，一般来说越靠近左边，移动的概率、距离越小，而越后面则越大（可以类比幽灵堵车）

我们能不能固定前面的对象，只移动后面的对象，从而实现压缩呢？（如果后面的对象和前面的对象大小一致，完全可以）

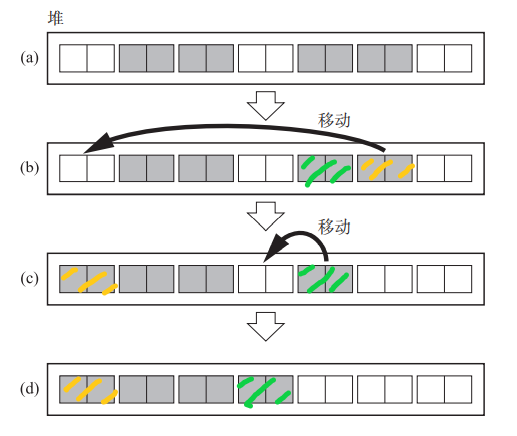
Two-Finger

表格算法

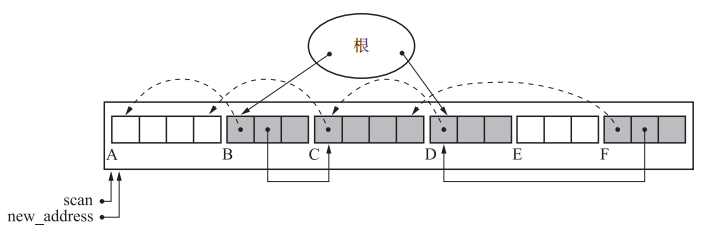
算法分为三部：移动对象群，构建间隙表格，更新指针

  • 移动对象群（Lisp2一次移动一个对象，这个一次移动所有相邻对象）

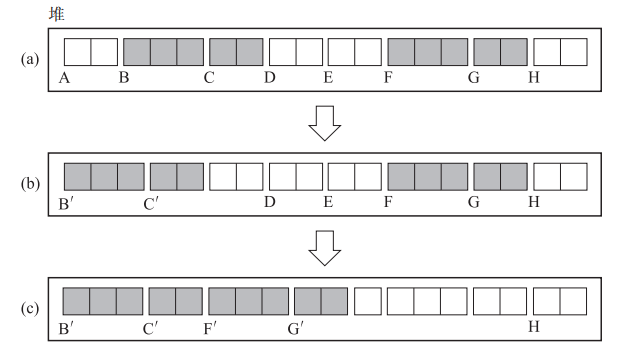
表格算法移动对象群

  • 构建间隙表格（设一个小格子尺寸为50）
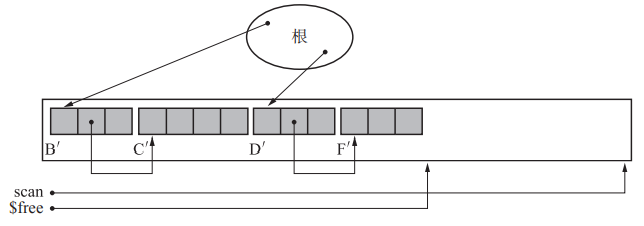
    • a到b：live在B开头，scan在D开头，于是将B的初始位置和B向左移动的距离$(100,100)$写到D处
    • b到c：
      • 先把间隙表格向后移动，移到FG之后，于是H处写入$(100,100)$
      • FG的初始位置和向左移动的距离为$(550,300)$，写入H之后（后是左边的G）

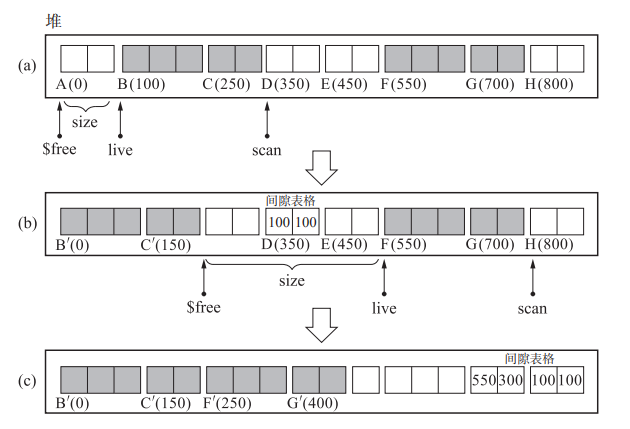
构建间隙表格

  • 更新指针

ImmixGC算法

六：保守式GC

把疑似指针的一律视为指针

不明确的根

常见的根有

  • 寄存器
  • 调用栈
  • 全局变量空间

在c++等语言里，int这种内置变量（非指针）和void*指针都存放在栈里，GC无法区分两者的区别，保守式GC就干脆不区分两者

存储着不确定对象的根，称为不明确的根，而基于这些根的GC算法，被称为保守式GC（ambiguous GC）

检查内容

  • 是否位对齐（32位CPU，指针是4的倍数，64位CPU，指针是8的倍数）
    • 不对齐的一定是非指针
  • 是否指向堆内
    • 对象放在堆中，所以指针一定指向堆
  • 是否指向对象开头

我们发现，有的时候我们会遇到一些格式与指针一致的非指针，我们称之为貌似指针的非指针（false pointer）

在标记清除算法中，遇到这种貌似指针的非指针，会胡乱找到一个对象，我们不知道这个对象是活动对象还是非活动对象，所以一律视为活动对象，进行标记

注意：保守GC是只有当判断不出来到底是不是指针时才将其视为指针，而不是把所有对象都视为指针（迫不得已，凑合凑合用）

评价

优点

  • 开发容易，程序员不需要意识到GC的存在

缺点

  • 识别指针和非指针需要付出代价（检查内容）
  • 将false pointer指向的错误对象视为活动对象，这些东西不会被用到，却进栈了
  • 支持保守GC的算法不多

准确式GC

正确的根（exact roots）可以精确地识别指针和非指针

基于正确的根的GC被称为准确式GC

构建正确的根的方法：打标签
  • 32位CPU指针的值是4的倍数，那么其低2位一定是0
  • 我们可以将所有非指针左移1位，然后将其低1位置为1
//打标签
int addTag(int a){
    a = a << 1;	//小心溢出，如果会溢出，就用一个更大的数据结构
	a = a|1;
    return a;
}
//去标签（在使用时需要恢复成正常数值），而且使用完后还有再次打标签
int getValue(int a){
    a  = a >> 1;
    return a;
}

除了打标签，还可以专门构建一个只存放指针的根，比如一些使用虚拟机（VM）的语言

评价

优点

  • 不需要判断是否为指针，没有判断带来的性能代价
  • 堆中只会存在指针，可以适用于一些移动对象的GC算法

缺点

  • 构建准确的根需要性能成本
  • 语言使用时更麻烦

间接引用

为什么保守式GC不能移动对象？因为一个false pointer可能是一个非指针，移动会导致问题

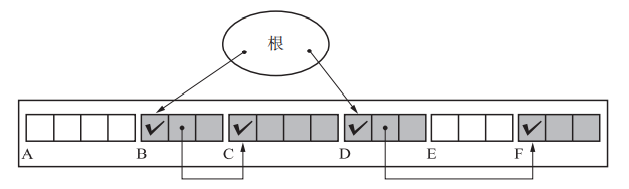
句柄

如图，即使我们移动了堆中的对象，也却不会改变根内的内容

句柄

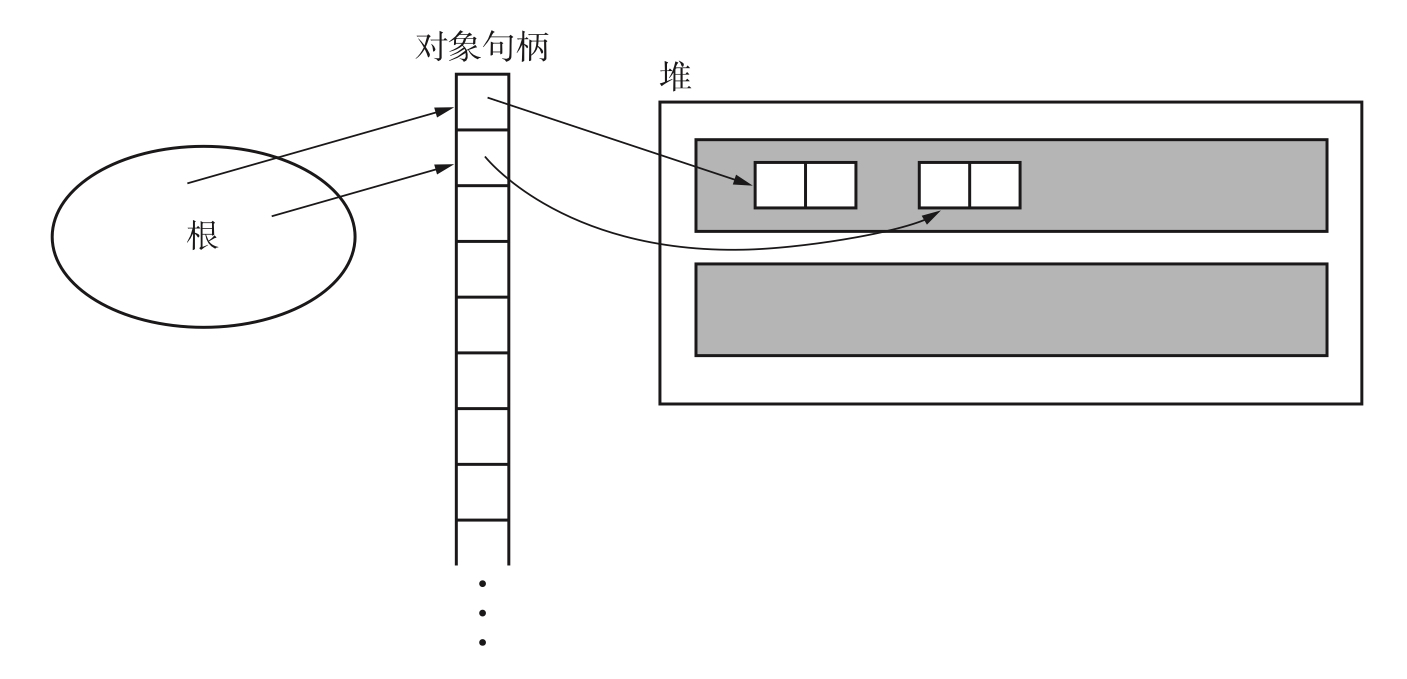
优点：

  • 可以使用复制算法

缺点：

  • 访问一个对象需要访问两次内存

MostlyCopyingGC

保守式GC复制算法

黑名单

有的false pointer即使是非指针，错把他当指针用也可以找到一个对象（尽管这个过程是未定义的），如果这个非指针可以做到这个事，拿我们就把这个非指针指向的地址存放到黑名单中

黑名单中存放的是地址，如果在这些地址中分配空间，可能会导致未定义事件

所以在这些地址上分配对象时要十分小心，比如只能分配小对象、只能分配没有子对象的小对象，因为这些对象比较小，即使变成垃圾，被错误识别了，危害也比较小

七：分代垃圾回收

引入了年龄这一概念，优先回收那些容易成为垃圾的对象

年龄

我们在引用计数法中提到过，绝大多数的对象生成后立刻会被回收，而被引用次数多多对象很难变成垃圾

于是我们引入年龄这一概念，初始为0，每经历一次GC算法，如果没有被回收，则年龄+1

我们发现年龄越大，说明对象越重要，越不容易被回收，于是年龄越大，参与回收的频率就越低

评价

优点

  • 提高吞吐量

缺点

  • 很多对象出生立刻回收只是一个经验，不适合所有程序，一旦某程序对象比较“长寿”，会起反作用

八：增量式垃圾回收

想一想单核CPU并行的本质，就是将线程切分，来回切换

通过逐步推进垃圾回收来控制最大暂停时间，不一次执行完GC，而是执行一会mutator，执行一会GC

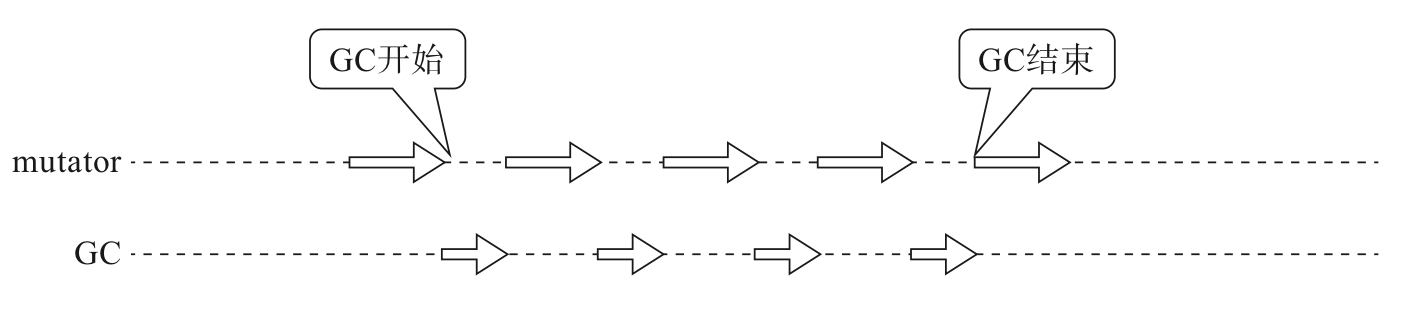
增量式GC
  • 三色标记法

评价

优点

  • 降低最大暂停时间

缺点

  • 降低了吞吐量

九：RC Immix算法

这是一个2013年的算法，听懂掌声

将合并型引用计数法和Immix组合到一起，改善了引用计数法的吞吐量

更新于：2024年7月3日

GC

评论