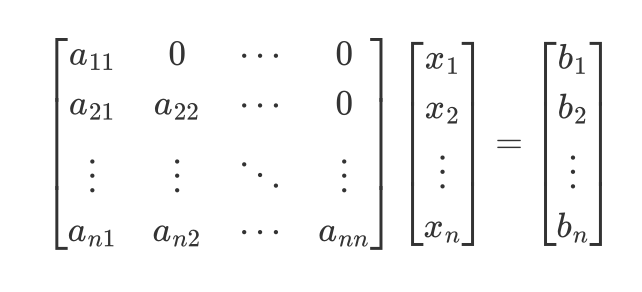Pro TBB

在摩尔定律逐渐失效的今日，CPU主频和单核性能提升越来越不明显，为了得到跟高的性能，我们走向了并行计算的道路

概念

并发和并行

并发（Concurrent）：happening during the same time span，处理器在两件事间快速切换，宏观上看，就像是同时发生的（下图AB）
并行（Parallel）：happening at the same time，多个处理器一起做事（下图CD）

TBB基础

TBB（Threading Building Blocks）是一个非常流行的C++并行编程（parallel programming）方案

使用Task而非Thread
- Thread与硬件相关，直接编写难以跨平台，而且线程间通信过于频繁，过于繁琐
- TBB使用Task编程，运行时会将程序映射到硬件上（该方法对嵌套并行的支持很不错）
- TBB任务调度使用工作窃取，当一个任务队列执行完毕后，核心会去其他任务队列中窃取任务，于是可以提高核心的利用率
TBB实现了可组合性（Composability）
- 简单来说就是支持for循环
方便移植（portable）

Mac上安装使用TBB

安装tbb

$brew install tbb

链接tbb

#寻找tbb包
find_package(TBB REQUIRED)
...
#链接
target_link_libraries(TimeStudy TBB::tbb)

引用头文件

#include<tbb/tbb.h>

在Ubuntu上安装TBB

$sudo apt-get install libtbb-dev

调用函数

template<typename Func0, [...,] typename FuncN>
void parallel_invoke(const Func0& f0, [...,] const FuncN& fN);

一个简单的TBB示例，并行输出两行字符串

通过tbb::parallel_invoke实现任务、函数粒度的并行

#include <iostream>
#include <tbb/tbb.h>

int main() {
    tbb::parallel_invoke(
            [](){std::cout << "TBB!" << std::endl;},
            [](){std::cout << "Hello" << std::endl;}
            );
    return 0;
}

我们这里使用lambda表达式创建了匿名（anonymous）函数，可以大幅简化TBB编写

快排示例

传统快排算法（升序）

在数列中取一个数作为基准数
比基准小的放在基准左边，大的放在右边
对左右两边分别快排，直到只剩一个数（左右重合）

能看出，这个算法采用了分治的思想，很适合并行

#include <iostream>
#include <vector>
#include <tbb/tbb.h>

using QV = std::vector<int>;
//传统快排
void quickSort(QV::iterator left, QV::iterator right){
    if(left >= right){ return; }
    int pivot_value = *left;
    QV::iterator i = left, j = right - 1;
    while(i != j){
        while(i != j && pivot_value < *j) --j;    //从右向左找，直到找到一个比基准小的
        while(i != j && pivot_value >= *i) ++i;   //从左往右找，直到找到一个比基准大的
        std::iter_swap(i, j);
    }
    std::iter_swap(left, i);
    quickSort(left, i);
    quickSort(j+1, right);
}
//并行快排
void parallelQuicksort(QV::iterator left, QV::iterator right){
    if(left >= right){ return; }
    int pivot_value =  *left;
    QV::iterator i = left, j = right - 1;
    while (i != j) {
        while (i != j && pivot_value < *j) --j;
        while (i != j && pivot_value >= *i) ++i;
        std::iter_swap(i, j);
    }
    std::iter_swap(left, i);

    // recursive call
    tbb::parallel_invoke(
      			//lambda表达式[=]表示传入当前函数所有的成员
            [=]() { parallelQuicksort(left, i); },
            [=]() { parallelQuicksort(i + 1, right); }
    );

}
//使用cutoff
void parallelCutoffQuicksort(QV::iterator left, QV::iterator right){
    const int cutoff = 100;

    if (right - left < cutoff) {
        quickSort(right, left);
    }
    else {
        int pivot_value =  *left;
        QV::iterator i = left, j = right - 1;
        while (i != j) {
            while (i != j && pivot_value < *j) --j;
            while (i != j && pivot_value >= *i) ++i;
            std::iter_swap(i, j);
        }
        std::iter_swap(left, i);

        // recursive call
        tbb::parallel_invoke(
                [=]() { parallelQuicksort(left, i); },
                [=]() { parallelQuicksort(i + 1, right); }
        );
    }
}

int main() {
    std::vector<int> nums;
    for(int i = 0; i < 5000; ++i){
        nums.push_back(rand() % 5000);
    }
  	//warmup
    tbb::parallel_for(0, 10, [](int) {
        tbb::tick_count t0 = tbb::tick_count::now();
        while ((tbb::tick_count::now() - t0).seconds() < 0.01);
    });

    std::vector<int> nums2 = nums;
    tbb::tick_count t0 = tbb::tick_count::now();
    quickSort(nums.begin(), nums.end());
    std::cout << "Normal Time=" << (tbb::tick_count::now() - t0).seconds() << std::endl;

    tbb::tick_count t1 = tbb::tick_count::now();
    parallelQuicksort(nums2.begin(), nums2.end());
    std::cout << "Parallel Time=" << (tbb::tick_count::now() - t1).seconds() << std::endl;
    return 0;
}

最后结果，当数组比较大的时候，并行快排速度会更快一点

Normal Time=0.0023285
Parallel Time=0.00110846

此外tbb进行任务分配也会有开销，因此我们往往将大任务分成若干个小任务后，让小任务串型执行，上文中的cutoff就是起到这个作用，这样往往能得到更高的性能

时刻查询

//t0时刻
tbb::tick_count t0 = tbb::tick_count::now();	
...
//当前时刻-t0时刻=经过了多长时间段（并转化为秒）
std::cout << "Time: " << (tbb::tick_count::now() - t0).seconds() << " seconds" << std::endl;

并行开发中动态内存管理十分复杂、危险（内存泄漏），这里推荐使用C++11的智能指针（自带GC）

Flow Graph

将函数执行制作成Graph，实现消息驱动的并行（有些类似FrameGraph）

void fig1_10(const std::vector<ImagePtr>& image_vector){
    const double tint_array[] = {0.75, 0, 0};

    tbb::flow::graph g;
    int i = 0;
    //注意，source_node已经失效
    tbb::flow::input_node<ImagePtr> src(g,
        [&i, &image_vector](tbb::flow_control &fc) -> ImagePtr {
            if(i < image_vector.size()){
                return image_vector[i++];
            }
            else{
                fc.stop();
                return {};
            }
    });
    tbb::flow::function_node<ImagePtr, ImagePtr> gamma(g,
        tbb::flow::unlimited, [] (ImagePtr img) -> ImagePtr{
                return applyGamma(img, 1.4);
        }
    );
    tbb::flow::function_node<ImagePtr, ImagePtr> tint(g,
        tbb::flow::unlimited, [tint_array] (ImagePtr img) -> ImagePtr{
                return applyTint(img, tint_array);
        }
    );
    tbb::flow::function_node<ImagePtr> write(g,
         tbb::flow::unlimited, [] (ImagePtr img){
                writeImage(img);
        }
    );

    tbb::flow::make_edge(src, gamma);
    tbb::flow::make_edge(gamma, tint);
    tbb::flow::make_edge(tint, write);
    src.activate();
    g.wait_for_all();
}

最后该程序会以流水线的形式执行，当第一张图片完成gamma矫正，去执行tint着色时，第二张图片开始执行gamma矫正（每张图片间互不影响）

相比于TimeStudy的串型执行，流水线执行效率会更快

循环

template<typename Index, typename Func>
Func parallel_for(Index frist, Index last, [Index step,] const Func& f);

上面的代码，我们将图片处理切分为几个小块，但小块内部仍然是单线程

我们注意到，在图片处理时，有一个很大的循环在遍历图片上的像素点，那么能不能并行做这件事？

我们并行处理每一行

tbb::parallel_for(0, height,
                  [&in_rows, &out_rows, width, gamma](int i){
                    for(int j = 0; j < width; ++j){
                      const ImageLib::Image::Pixel& p = in_rows[i][j];
                      double v = 0.3 * p.bgra[2] + 0.59 * p.bgra[1] + 0.11 * p.bgra[0];
                      double res = pow(v, gamma);
                      if(res > ImageLib::MAX_BGR_VALUE){
                        res = ImageLib::MAX_BGR_VALUE;
                      }
                      out_rows[i][j] = ImageLib::Image::Pixel(res, res, res);
                    }
                  }
                 );

tbb::parallel_for(0, height,
                  [&in_rows, &out_rows, width, tints](int i){
                    for(int j = 0; j < width; ++j){
                      const ImageLib::Image::Pixel& p = in_rows[i][j];
                      std::uint8_t b = (double)p.bgra[0] + (ImageLib::MAX_BGR_VALUE - p.bgra[0]) * tints[0];
                      std::uint8_t g = (double)p.bgra[0] + (ImageLib::MAX_BGR_VALUE - p.bgra[1]) * tints[1];
                      std::uint8_t r = (double)p.bgra[0] + (ImageLib::MAX_BGR_VALUE - p.bgra[2]) * tints[2];
                      out_rows[i][j] = ImageLib::Image::Pixel(
                        (b > ImageLib::MAX_BGR_VALUE) ? ImageLib::MAX_BGR_VALUE : b,
                        (g > ImageLib::MAX_BGR_VALUE) ? ImageLib::MAX_BGR_VALUE : g,
                        (r > ImageLib::MAX_BGR_VALUE) ? ImageLib::MAX_BGR_VALUE : r
                      );
                    }
                  }
                 );

M1 Mac Xcode Clang至今不支持C++17的std::execution，对OpenMP的支持也相当差

归约

template<typename Range, typename Value, typename Func, typename Reduction>
Value parallel_reduce(const Range& range, const Value& identity, const Func& func, const Reduction& reduction);

树形规约

求最大值

下面是一个vector求最大值的示例，实现机制就是将整个数组分成一个个小块（chunks），分别对小块求最值，然后将小块归约（reduce），最后求得最值（形成了一个树型结构）

int pmax(const std::vector<int> &arr){
    int max_value = tbb::parallel_reduce(
      			//range，扫描范围
            tbb::blocked_range<int>(0, arr.size()),	
      			//identity，小块数据的初始值，这里赋值为int类型的最小值-2147483648
            std::numeric_limits<int>::min(),	
      			//func，每个小块的处理方式
            [&](const tbb::blocked_range<int> &r, int init) -> int{	
                for(int i = r.begin(); i != r.end(); ++i){
                    init = std::max(init, arr[i]);
                }
                return init;
            },
      			//reduction，小块间合并的处理方式
            [](int x, int y) -> int{
                return std::max(x, y);
            }
    );
    return max_value;
}

下面这是一个求PI的示例

double calcPI(int degree){
    double dx = 1.0 / degree;
    double sum = tbb::parallel_reduce(
      			//range，扫描范围
            tbb::blocked_range<int>(0, degree),
      			//identity，小块数据的初始值，这里赋值为0
            0.0,
      			//func，每个小块的处理方式
            [=](const tbb::blocked_range<int> &r, double init) -> double{
                for(int i = r.begin(); i != r.end(); ++i){
                    double x = (i + 0.5)*dx;
                    double h = std::sqrt(1 - x*x);  //勾股定理
                    init += h * dx;
                }
                return init;
            },
      			//reduction，小块间合并的处理方式
            [](double x, double y) -> double{
                return x+y;
            }
        );
    return 4 * sum;
}

扫描

template<typename Range, typename Value, typename Scan, typename Combine>
Value parallel_scan(const Range& range, const Value& identity, const Scan& scan, const Combine& combine);

前缀和

前缀和在图形领域也有很大的用处

对于一个数组，我们将其分为三个小块ABC

A.init=0, B.init=0
scan(A), scan(B)

B.init = A.ans
C.init = A.ans + B.ans
scan(B), scan(C)

最后我们只用了串行2/3的扫描时间，但是多做了1/3的扫描工作，时间减少了，但是工作量变大了

int parallelPrefix(const std::vector<int> &v, std::vector<int> &psum){
    int N = v.size();
    psum[0] = v[0];
    int final_sum = tbb::parallel_scan(
      			//range
            tbb::blocked_range<int>(1, N),
      			//identity
            (int)0,
      			//scan body
            [&v, &psum](const tbb::blocked_range<int> &r, int sum, bool is_final_scan) -> int{
                for(int i = r.begin(); i < r.end(); ++i){
                    sum += v[i];
                    if(is_final_scan){
                        psum[i] = sum;
                    }
                }
                return sum;
            },
      			//combine body
            [](int x, int y){
                return x+y;
            }
        );
    return final_sum;
}

可见性

如图，等间距摆放一个个薄板（厚度忽略不计），从最右上角向左看，能看到哪些薄板？

解题的本质就是比较夹角大小，只要夹角一直递增，就能看到

void visibility(const std::vector<double> &heights, std::vector<bool> & visible, double dx){
    const int N = heights.size();
    double max_angle = std::atan2(dx, heights[0] - heights[1]);

    double final_max_angle = tbb::parallel_scan(
      			//range
            tbb::blocked_range<int>(1, N),
      			//identity
            0.0,
      			//scan body
            [&heights, &visible, dx](const tbb::blocked_range<int> &r, double max_angle, bool is_final_scan) -> double {
                for(int i = r.begin(); i != r.end(); ++i){
                    double my_angle = atan2(i * dx, heights[0] - heights[i]);
                    if(my_angle >= max_angle){
                        max_angle = my_angle;
                    }
                    else if(is_final_scan){
                        visible[i] = false;
                    }
                }
                return max_angle;
            },
      			//combine body
            [](double a, double b){
                return std::max(a, b);
            }
        );
}

parallel_for_each

parallel_for在使用时必须指定range，但如果要处理的item数量不确定（比如在执行过程中修改itemList），那么就不能使用，这个时候我们可以使用parallel_for_each

template <typaname InputIterator, typename Body>
void parallel_for_each( InputIterator first, InputIterator last, Body body );

下面是一个遍历树的示例，若一个节点的v.first为prime，将其v.second修改为true。我们不知道树有多大，于是采用递归遍历

void f(PrimesTreeElement::Ptr root){
  PrimesTreeElement::Ptr tree_arry[] = {root};
  //tbb::parallel_do已经废弃
  tbb::parallel_for_each(
        tree_array,
        [](PrimesTreeElement::Ptr e, 
        //tbb::parallel_do_feeder已被废弃
        tbb::feeder<PrimesTreeElement::Ptr>& feeder){
        if(e){
          if(isPrime(e->v.first)) e->v.second = true;
          if(e->left) feeder.add(e->left);
          if(e->right) feeder.add(e->right);
        }
      }                 
  );
}

前向替换

前向替换（Forward Substitution）是线性代数中一种求解线性方程组的方法

一般解线性方程组有两种方法：

直接法
- 高斯消元法
- LU分解法
迭代法

高斯消元法：初中就学了，就是两个方程变化后相加减（也可以换元），消除变量，直到得到解。这个方法可以拓展到矩阵中，就是把线性方程转化为行阶梯矩阵（中间那个矩阵），然后简化为简化行阶梯矩阵（右边那个矩阵）

$$
\left[
\begin{matrix}
2 & 1 & -1 &|& 8 \\
-3 & -1 & 2 & | & -11 \\
-2 & 1 & 2 & | & -3
\end{matrix}
\right]
=>
\left[
\begin{matrix}
2 & 1 & -1 &|& 8 \\
0 & 1/2 & 1/2 & | & 1 \\
0 & 0 & -1 & | & 1
\end{matrix}
\right]
=>
\left[
\begin{matrix}
1 & 0 & 0 &|& 2 \\
0 & 1 & 0 & | & 3 \\
0 & 0 & 1 & | & -1
\end{matrix}
\right]
$$

前向替换法就是得到行阶梯矩阵后

能写出以下式子

$$
\begin{cases}
x_1 = b_1/a_{11} \\
x_2 = (b_2-a_{21}x_1)/a_{22} \\
\ \vdots \\
x_n = (b_n -a_{n1}x_1-a_{n2}x_2 - \cdots -a_{nn-1}x_{n-1})/a_{nm}
\end{cases}
$$

于是我们只需要从第一个式子开始，逐步向下替换，就能求出方程的解

如果是下三角矩阵，那就是后向替换

//a是一个下三角矩阵，x、b是向量
void serialFS(std::vector<double>& x, const std::vector<double>& a, std::vector<double>& b) {
    const int N = x.size();
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < i; ++j) {
            b[i] -= a[j + i*N] * x[j];
        }
        x[i] = b[i] / a[i + i*N];
    }
}

加入分块和并行后：

void parallelFS(std::vector<double> &x, const std::vector<double> &a,
                std::vector<double> &b) {
  const int N = x.size();
  const int block_size = 512;
  const int num_blocks = N / block_size;
  //tbb::atomic已经废弃
  std::vector<std::atomic<char>> ref_count(num_blocks * num_blocks);
  for (int r = 0; r < num_blocks; ++r) {
    for (int c = 0; c <= r; ++c) {
      if (r == 0 && c == 0)
        ref_count[r * num_blocks + c] = 0;
      else if (c == 0 || r == c)
        ref_count[r * num_blocks + c] = 1;
      else
        ref_count[r * num_blocks + c] = 2;
    }
  }

  using BlockIndex = std::pair<size_t, size_t>;
  BlockIndex top_left(0, 0);
  //tbb::parallel_do已经废弃
  tbb::parallel_for_each(&top_left, &top_left + 1,
                         [&](const BlockIndex &bi, tbb::feeder<BlockIndex> &feeder) {
                           size_t r = bi.first;
                           size_t c = bi.second;
                           int i_start = r * block_size, i_end = i_start + block_size;
                           int j_start = c * block_size, j_max = j_start + block_size - 1;
                           for (int i = i_start; i < i_end; ++i) {
                             int j_end = (i <= j_max) ? i : j_max + 1;
                             for (int j = j_start; j < j_end; ++j) {
                               b[i] -= a[j + i * N] * x[j];
                             }
                             if (j_end == i) {
                               x[i] = b[i] / a[i + i * N];
                             }
                           }
                           // add successor to right if ready
                           if (c + 1 <= r && --ref_count[r * num_blocks + c + 1] == 0) {
                             feeder.add(BlockIndex(r, c + 1));
                           }
                           // add succesor below if ready
                           if (r + 1 < (size_t) num_blocks && --ref_count[(r + 1) * num_blocks + c] == 0) {
                             feeder.add(BlockIndex(r + 1, c));
                           }
                         }
                        );
}

流水线

void parallel_pipeline( size_t max_number_of_live_tokens, const filter<void,void>& filter_chain );

template<typename T, typename U, typename Func>
filter_t<T, U> make_filter(filter::mode mode, const Func& f);

管线（pipeline）是过滤器（filters）的线性序列，物体（items）在通过过滤器时，会被处理

//并行 将字符串中大写变小写
void fig_2_27(int num_tokens, std::ofstream &caseBeforeFile, std::ofstream &caseAfterFile) {
  tbb::parallel_pipeline(
    //tokens
    num_tokens,
    //第一个filter，负责创建字符串
    tbb::make_filter<void, CaseStringPtr>(
        //tbb::filter::serial_in_order已经废弃
        tbb::filter_mode::serial_in_order,
        //filter body
        [&](tbb::flow_control &fc) -> CaseStringPtr {
            CaseStringPtr s_ptr = getCaseString(caseBeforeFile);
            if (!s_ptr)
              fc.stop();
            return s_ptr;
        }) 
    
    & // 链接
    
    //第二个filter，负责修改字符串
    tbb::make_filter<CaseStringPtr, CaseStringPtr>(
        //filter node
        tbb::filter_mode::parallel,
        //filter body
        [](CaseStringPtr s_ptr) -> CaseStringPtr {
        		std::transform(s_ptr->begin(), s_ptr->end(), s_ptr->begin(),
                       [](char c) -> char {
                         if (std::islower(c))
                           return std::toupper(c);
                         else if (std::isupper(c))
                           return std::tolower(c);
                         else
                           return c;
                       });
        		return s_ptr;
      }) 
    
      & //链接
    
      //第三个filter，负责写字符串
    	tbb::make_filter<CaseStringPtr, void>(
          //filter node
          tbb::filter_mode::serial_in_order,
          //filter body
          [&](CaseStringPtr s_ptr) -> void {
            	writeCaseString(caseAfterFile, s_ptr);
          })
      );
}

Flow Graphs

并行编程另一个问题是混乱，传统并行编程为了避免程序混乱（messy），我们需要事无巨细地管理每一件事。但在上一节简单提到的Flow Graphs，提供了一个简单的管理方法

Flow Graphs允许我们用图（DAG）来描述程序，相比于parallel_do和parallel_pipeline，FlowGraphs自由度更高，推荐使用。

每个节点是一个并行函数，箭头代表数据的流向/消息传递，我们将这个图称为数据流向图（data flow graphs）
图也可以描述操作的前后顺序，进而可以构建一些传统方法难以表示的独立结构体，这种图被称为依赖图（dependency graphs）

预热

static void warmupTBB() {
    //tbb::task_scheduler_init::default_num_threads()已经弃用
    tbb::parallel_for(0, tbb::this_task_arena::max_concurrency(), [](int) {
        tbb::tick_count t0 = tbb::tick_count::now();
        while ((tbb::tick_count::now() - t0).seconds() < 0.01);
    });
}

无论是web服务器、CPU/GPU并行计算，深度学习，都有warmup的概念

对于一个项目，如果采用冷启动的方式，从零瞬间增加计算量，可能会把系统压垮，于是我们可以使用warmup，逐步提高项目负荷。

数据流图

构建图对象
创建节点，填充节点信息
链接节点
发送消息
等待图完成

void graphSample(){
    //创建图对象
    tbb::flow::graph g;
    //创建节点
    tbb::flow::function_node<int, std::string> my_first_node(
            g, tbb::flow::unlimited,
            [](const int &in) -> std::string{
                std::cout << "first node received: " << in << std::endl;
                return std::to_string(in);
            }
        );
    tbb::flow::function_node<std::string> my_second_node(
            g, tbb::flow::unlimited,
            [](const std::string &in){
                std::cout << "second node received: " << in << std::endl;
            }
        );
    //链接
    tbb::flow::make_edge(my_first_node, my_second_node);
    //发送消息
    my_first_node.try_put(10);
    //等待图完成
    g.wait_for_all();
}

节点

Flow Graphs有三种节点

functional
control flow
buffering

function_node

template<typename Body>
function_node(graph& g, size_t concurrency, Body body);

函数节点，当消息传递到该节点，会被函数处理，并将输出值传递给后继者

//输入一个int类型，输出一个std::string类型
tbb::flow::function_node<int, std::string> my_first_node(
  					//图对象
            g, 	
  					//节点的并发限制，0是无限制(unlimited)，1是串行(serial)
  					tbb::flow::unlimited,	
  					//body
            [](const int &in) -> std::string{
                std::cout << "first node received: " << in << std::endl;
                return std::to_string(in);
            }
        );

函数节点可以从他所连接（edges）其他节点获取消息，也可以使用try_put手动向其传递消息

join_node

template <typename Body, typename... Bodies>
join_node(graph&, Body, Bodies...)->join_node<std::tuple<std::decay_t<input_t<Body>>, std::decay_t<input_t<Bodies>>...>, key_matching<output_t<Body>>>;

流控制节点，当消息传递到该节点，会创建一个消息元组（tuple），然后将元组广播给所有后继者

//my_node，输入int，输出std::string
tbb::flow::function_node<int, std::string> my_node{...};
//my_other_node，输入int，输出double
tbb::flow::function_node<int, double> my_other_node{...};
//join节点，这里的作用是将两个节点的输出整合，传递给my_final_node
tbb::flow::join_node<std::tuple<std::string, double>,
            tbb::flow::queueing> my_join_node{g};
//my_final_node，输入一个元组
tbb::flow::function_node<std::tuple<std::string, double>, int> my_final_node{g,
                   tbb::flow::unlimited,
                   [](const std::tuple<std::string, double>& in) -> int {
                     std::cout << "final: " << std::get<0>(in)
                       << " and " << std::get<1>(in) << std::endl;
                     return 0;
                   }
                  };

有的时候，我们需要保证join_node的输入的对应的。比如我想将两张照片拼成一张，我开两个节点并行读项目，再用join_node整合后传入merge函数节点，然而在这个过程中，我必须保证传入的两个像素点在同一位置，为此，我们可以添加一个frameNumber做标记（tags）

//使用函数对象作为tags，可以用input_port<i>读出来
tbb::flow::join_node<std::tuple<Image, Image>, tbb::flow::tag_matching >
    join_images_node(g, [] (Image left) { return left.frameNumber; },
                        [] (Image right) { return right.frameNumber; } );
...
tbb::flow::make_edge(increase_left_node, tbb::flow::input_port<0>(join_images_node));
tbb::flow::make_edge(increase_right_node, tbb::flow::input_port<1>(join_images_node));
tbb::flow::make_edge(join_images_node, merge_images_node);

链接

template<typename Message>
    inline void make_edge( sender<Message> &p, receiver<Message> &s );
template< typename MultiOutputNode, typename MultiInputNode >
    inline void make_edge( MultiOutputNode& output, MultiInputNode& input );

我们可以使用make_edge链接两个节点

//这里的input_port是一种sender，跟节点差不多，都能互相链接
make_edge(my_node, tbb::flow::input_port<0>(my_join_node));
make_edge(my_other_node, tbb::flow::input_port<1>(my_join_node));
make_edge(my_join_node, my_final_node);

激活

为了激活图，我们需要向图中传递消息，除了前文的try_put，我们也可以使用input_port

//my_node是一个input_node
my_node.activate();	//将其设为活动状态，启用消息生成

等待

g.wait_for_all();

性能限制

Flow Graphs是一个基于Task的并行框架，当消息到达一个节点时，根据节点的并发限制，创建Task。生成的Task会进一步映射为线程（跟上一节讲的循环、算法的机制一样）

真正限制Flow Graphs性能的有

串行节点（serial node）
工作线程数
任务复杂度

依赖图

很像RenderGraph

	数据流向图	依赖图
Edges含义	表示数据流向	表示节点的先后顺序
信息传递方式	消息	shared memory
节点类型	function_node	continue_node

节点的先后顺序，描述的是依赖关系，只有前面节点执行结束后，后面节点才能安全、正确地执行
依赖图不使用函数节点，而是继续节点continue_node，节点间的消息传递使用，当传入continue_node的消息（continue_msg）数量等于该节点需要的消息数量，节点内的函数会开始执行
continue_node只关心传入的消息数量，不关心消息源。这导致依赖图必须是非循环的（acyclic），因为一个物体循环发出两次消息，（在这里）等同于两个物体各发出一次消息

构建依赖图

创建图对象
创建节点
链接
发送信息
等待图完成

前向替换

之前我们使用parallel_for_each实现了一份前向替换，我们现在用依赖图再实现一次

经观察，我们发现辅对角线的块/迭代器是相互独立的，他们之间没有依赖关系（上图(b)，块BC间没有依赖，他们只需要在A之后执行就可以正确运算）

经观察，同时并行计算的最大块数为辅对角线的长度，也就是图中标注的 a set of independent blocks

经观察，上图(b)中每一个块需要接受两个msg，正好与block_sizes大小相等

using Node = tbb::flow::continue_node<tbb::flow::continue_msg>;
using NodePtr = std::shared_ptr<Node>;
NodePtr createNode(tbb::flow::graph &g, int r, int c, int block_size,
                   std::vector<double> &x, const std::vector<double> &a, std::vector<double> &b);
void addEdges(std::vector<NodePtr> &nodes, int r, int c, int block_size, int num_blocks);
void dependencyGraphFS(std::vector<double> &x, const std::vector<double> &a, std::vector<double> &b){
    const int N = x.size();
    const int block_size = 1024;
    const int num_blocks = N / block_size;
		//创建num_blocks * num_blocks个节点，只不过我们只会用到下半部分
    std::vector<NodePtr> nodes(num_blocks * num_blocks);
    //创建图对象
    tbb::flow::graph g;
  	//我们从最下面一行开始向上构建
    for(int r = num_blocks-1; r >= 0; --r){
        for(int c = r; c >= 0; --c){
            //创建图节点
            nodes[r * num_blocks + c] = createNode(g, r, c, block_size, x, a, b);
            //链接
            addEdges(nodes, r, c, block_size, num_blocks);
        }
    }
    //传入消息
    nodes[0]->try_put(tbb::flow::continue_msg());
    //等待完成
    g.wait_for_all();
}

NodePtr createNode(tbb::flow::graph &g, int r, int c, int block_size,
                   std::vector<double> &x, const std::vector<double> &a, std::vector<double> &b){
    const int N = x.size();
    return std::make_shared<Node>(
            g,
            [r, c, block_size, N, &x, &a, &b](const tbb::flow::continue_msg & msg){
                int i_start = r * block_size, i_end = i_start + block_size;
                int j_start = c * block_size, j_max = j_start + block_size -1;
                //对于每个块，串行进行正向替换计算
                for(int i = i_start; i < i_end; ++i){
                    int j_end = (i <= j_max) ? i : j_max+1;
                    for(int j = j_start; j < j_end; ++j){
                        b[i] -= a[j + i*N] * x[j];
                    }
                    if(j_end == i){
                        x[i] = b[i] / a[i + i*N];
                    }
                }
                return msg;
            }
        );
}

void addEdges(std::vector<NodePtr> &nodes, int r, int c, int block_size, int num_blocks){
    NodePtr np = nodes[r * num_blocks + c];
  	//每个块链接自己的下面和右边，最下面和最右边不链接
    if(c + 1 < num_blocks && r != c){
        tbb::flow::make_edge(*np, *nodes[r * num_blocks + c + 1]);
    }
    if(r + 1 < num_blocks){
        tbb::flow::make_edge(*np, *nodes[(r+1) * num_blocks + c]);
    }
}

PSTL

parallel_sort

同步

在并行编程中，我们要极力避免同步（Synchronization）和互斥（exclusion），这会严重影响性能

但是很多情况下，我们不得不同步，书中称其为“必要之恶”（necessary evil）

写冲突

比如我们想要统计一张图中各种颜色出现的次数，如果是串行处理，我们就遍历每一个像素，用一个数组存储统计值

for(int i = 0; i < N; ++i){
  hist[image[i]]++;
}

但当我们想要并行处理遍历像素时，就会出现问题。如果两个线程同时读到了同一种颜色，于是都想执行hist[p]++，而如果该操作不支持原子（atomic）操作，就会出现写冲突

RMW

现代操作系统将很多操作设置为原子操作，该操作被视为一个完成的操作，不可分割，因此是线程安全的。比如对齐读（Aligned Read），对齐写（Aligned Write）

原子的本意就是不可分割的意思，当年化学家和物理学家认为原子是最小的粒子（尽管并非如此）

Read-Modify-Write（RMW）设计原则，可以让复杂操作原子化，当多个线程想要对某个内存进行修改时，保证线程安全并只执行一次

windows原子操作的实现原理（_InterlockedIncrement）

读内存
计算得到新值
若内存位置仍然是原始值，则将新值写入该内存位置
- 若不是原始值，则在下一个循环周期中重新操作

锁

解决并行写冲突最简单的方法就是加锁，我们给对象加一个互斥锁（mutex），写之前上锁，写完解锁，其他线程无法操作锁住的对象。而上锁解锁操作中间的代码被称为临界区（critical section），是被锁保护的部分。

锁会影响性能

//tbb::task_scheduler_init init{nth}已经弃用，用于设置最大线程数
tbb::global_control global_limit(tbb::global_control::max_allowed_parallelism, nth);

using my_mutex_t=tbb::spin_mutex;
my_mutex_t my_mutex;
std::vector<int> hist_p(num_bins);
parallel_for(tbb::blocked_range<size_t>{0, image.size()},
             [&](const tbb::blocked_range<size_t>& r)
             {
                 //这种写法比my_lock.acquire(my_mutex)、my_lock.release()好
                 my_mutex_t::scoped_lock my_lock{my_mutex};
                 for (size_t i = r.begin(); i < r.end(); ++i)
                   	hist_p[image[i]]++;
             });

原子操作

锁过于消耗性能，原子操作效果会好一些，只不过这样还是比线性慢，而且不是真共享（Sharing）

什么是原子？原子的原意就是不可分割的基本粒子，我们在实现a++时，本质是分了三步

取a
加法运算
写a

由于并行计算，其他线程可能在你完整完成这三步期间进行操作，于是就会出现冲突。而原子操作就是将这三步视为一步，不可分割，在完整完成这三部之前，其他线程无权访问，等到操作结束

std::vector<std::atomic<int>> hist_p2(num_bins);
parallel_for(tbb::blocked_range<size_t>{0, image.size()}, 
             [&](const tbb::blocked_range<size_t>& r)
             {
                 for(size_t i = r.begin(); i < r.end(); ++i)
                 {
                     hist_p2[image[i]]++;
                 }
             }
            );

Thread Local Storage

一个较好的解决方案是私有化（Privatization）和归并（Reduction）

我感觉这个的设计理念就是：如果不得不同步，那就尽可能让更多更复杂的计算并行执行，最后对统一、规范、简单的数据进行同步

前面并行统计Image像素信息时，会出现多个线程写冲突。但如果让每个线程都有一个Image副本，线程对自己的副本进行操作（私有化），最后将这些副本进行归并。

私有化确实不会出现写冲突了，尽管归并仍然存在同步问题，但这个归并更简单，毕竟归并几个数，远远比处理几个线程冲突要简单，性能开销小

TBB提供了多种私有化+归并的的方案，其中归并模板（parallel_reduce）在TBB基础时就讲了

Thread Local Storage（TLS）：让每一个线程拥有一份副本，只不过存储开销过大，不宜过多使用
- enumerable_thread_specific（ETS）
- combinable

ETS

tbb::enumerable_thread_specific<T>对象是一个大容器，容器内包含者每一个线程所对应的副本，我们可以使用迭代器进行访问

using vector_t = std::vector<int>;
using priv_h_t = tbb::enumerable_thread_specific<vector_t>;
priv_h_t priv_h{num_bins};
//私有化
parallel_for(tbb::blocked_range<size_t>{0, image.size()},
             [&](const tbb::blocked_range<size_t>& r)
             {
                 //若该线程第一次使用local，那么会创建一个新的vector<int>，初始值为0
                 priv_h_t::reference my_hist = priv_h.local();
                 for (size_t i = r.begin(); i < r.end(); ++i){
                     //my_hist是引用，实际上是在修改priv_h[xxx]，以此将数据传递到线程外
                     my_hist[image[i]]++;
                 }     
             });
//归并
vector_t hist_p3(num_bins);
for(auto i=priv_h.begin(); i!=priv_h.end(); ++i){
    for (int j=0; j<num_bins; ++j) {
    	hist_p3[j]+=(*i)[j];
    }
}

使用STL算法替代循环，进行归并

//我们可以使用transform替代循环遍历
for (auto& i: priv_h) { // i traverses all private vectors
    std::transform(hist_p3.begin(),    // source 1 begin
                   hist_p3.end(),      // source 1 end
                   i.begin(),          // source 2 begin
                   hist_p3.begin(),    // destination begin
                   std::plus<int>() ); // binary operation
	}

由于归并过于常用，TBB也对归并做了封装

//使用combine_each
priv_h.combine_each([&](vector_t i){
        std::transform(hist_p3.begin(),   	// source 1 begin
                   hist_p3.end(),      		// source 1 end
                   i.begin(),         		// source 2 begin
                   hist_p3.begin(),    		// destination begin
                   std::plus<int>() );		// binary operation
    });
//或者使用combine
vector_t hist_p = priv_h.combine([](vector_t a, vector_t b) -> vector_t {
      std::transform(a.begin(),         // source 1 begin
                     a.end(),           // source 1 end
                     b.begin(),         // source 2 begin
                     a.begin(),         // destination begin
                     std::plus<int>() );// binary operation
       return a;
    });

combinable

combinable<T>对象也是一个容器，每一个线程对应一个instance

但是与ETS不同，combinable<T>并不能使用迭代器访问，这样设计的目的是不向外暴露对象，这样归并结束后大容器和其中的数据都释放了，以此节省局部空间

//combinable
tbb::combinable<vector_t> priv_h2{[num_bins](){return vector_t(num_bins);}};
//私有化
parallel_for(tbb::blocked_range<size_t>{0, image.size()},
             [&](const tbb::blocked_range<size_t>& r)
             {
                 vector_t& my_hist = priv_h2.local();
                 for (size_t i = r.begin(); i < r.end(); ++i)
                     my_hist[image[i]]++;
             });
//归并
vector_t hist_p4(num_bins);
priv_h2.combine_each([&](vector_t i)
                     { // for each priv histogram a
                         std::transform(hist_p4.begin(),     // source 1 begin
                                        hist_p4.end(),      // source 1 end
                                        i.begin(),          // source 2 begin
                                        hist_p4.begin(),    // destination begin
                                        std::plus<int>() ); // binary operation
                     });

最终性能比较，能看出TLS能大幅提高性能

Serial:       0.399203
Parallel:     2.01466
Atomic:       0.500326
ETC:          0.0348115
combinable:   0.0339478

parallel_reduce

最简单的归并，还是给用tbb封装好的模板，该算法的本质是树形规约

//parallel_reduce
using image_iterator = std::vector<uint8_t>::iterator;
t0 = tbb::tick_count::now();
vector_t hist_p5 = parallel_reduce (
    /*range*/    
    tbb::blocked_range<image_iterator>{image.begin(), image.end()},
    /*identity*/ 
    vector_t(num_bins),
    // 1st Lambda: Parallel computation on private histograms
    [](const tbb::blocked_range<image_iterator>& r, vector_t v) {
        std::for_each(r.begin(), r.end(),
                      [&v](uint8_t i) {v[i]++;});
        return v;
    },
    // 2nd Lambda: Parallel reduction of the private histograms
    [num_bins](vector_t a, const vector_t & b) -> vector_t {
        for(int i=0; i<num_bins; ++i) a[i] += b[i];
        return a;
});

并发容器

在上一节我们遇到了同步问题，处理同步会大幅降低性能，为此我们使用了TLS等方法实现了高效的显式同步，而这一节，我们将介绍TBB的核心，并发（Concurrent）

TBB提供了一些高效、线程安全的并发容器，他们大多是使用细粒度的锁或者无锁设计

细粒度锁：指锁定真正需要锁定的地方（其实还是挺低效的），比如一个数组我们只锁我们需要的某一个元素，其他线程如果不访问我这个元素，就能正常并行
无锁：有的线程负责操作，有的线程负责纠错

TBB的并发容器并发性能很好，但串行性能不如STL

顺序表（Sequences）
- concurrent_vector
队列（Queues）
- concurrent_queue
- concurrent_bounded_queue
- concurrent_priority_queue
无序关联容器（Unordered associative containers）
- concurrent_hash_map
- map/multimap
- set/multiset
有序关联容器（Ordered associative containers）
- map/multimap
- set/multiset

concurrent_hash_map

template <typename Key, typename T,
                 typename HashCompare = tbb_hash_compare<Key>,
                 typename Allocator = tbb_allocator<std::pair<const Key, T>>>
class concurrent_hash_map {..}

这是一个字符串-Int的哈希表

//HashCompare必须有hash函数和equal函数
struct MyHashCompare{
    static size_t hash(const std::string& s){
        size_t h = 0;
        for(auto &c : s){
            h = (h*17)^c;
        }
        return h;
    }
    static bool equal(const std::string& x, const std::string& y){
        return x == y;
    }
};
//hash map
typedef tbb::concurrent_hash_map<std::string, int, MyHashCompare> StringTable;
//一个函数对象，用于记录table内元素数量
class Tally{
private:
    StringTable& table;
public:
    Tally(StringTable& table_): table(table_) {}
    void operator() (const tbb::blocked_range<std::string*> range) const {
        for(std::string* p = range.begin(); p != range.end(); ++p){
          	//accessor类似于锁、智能智能，在accessor完成前，其他线程不能lookup这个key
            StringTable::accessor a;
            table.insert(a, *p);
            a->second += 1;
        }
    }
};

int main() {
    StringTable table;
    tbb::parallel_for( tbb::blocked_range<std::string*>( Data, Data+N, 1000 ), Tally(table) );

    for( StringTable::iterator i=table.begin();
         i!=table.end();
         ++i )
        printf("%s %d\n",i->first.c_str(),i->second);
    return 0;
}

内存分配

内存分配最重要的是正确，TBB提供了一套可拓展的内存分配

现代C++推荐使用智能指针进行内存管理，不推荐使用malloc和new。TBB完全适配所有版本的C++标准，也推荐使用智能指针进行内存分配

TBB动态内存分配的核心是线程内存池（memory pooling by threads），该内存池可以避免内存分配带来的性能下降，也不苛求“避免cache间不必要的数据移动”

TBB还提供了可拓展的缓存对齐，比std::aligned_alloc使用更简单方便。只不过滥用缓存对齐可能会带了巨大的内存浪费

在并行编程中，内存分配的主要问题是：分配器的争用，缓存效果

分配器争用：C++内存分存储在两个位置，堆和栈。传统的非线程分配器只能在单个全局堆中分配和释放内存，这个过程配合锁以实现互斥，很低效
缓存效应：某些操作可能会把缓存中的数据移动到缓存的另一处，这是很无效的行为，要避免

缓存填充（对齐）

用于解决假共享（我们在同步那一节解决了真共享带来的问题）

基于局部性原则，当CPU查询某个数据时：

若cache中没有找到，就会去内存中寻找
找到后会将该数据写入cache（时间局部性，刚刚被引用过的一个内存位置容易再次被引用）
并将其相邻元素也写入cache（空间局部性，一个内存位置被引用，其相邻位置很可能马上被引用）

如上图，CPU访问a时，先去cache去找，如果cache中没有，就会去内存中寻找，找到后将a和相邻的b写入cache的同一行。但问题出现了，如果当前cache的其他行里，已经有b了呢？

另一个线程也拥有一缓存行，里面存储了b，结果b却被移动到a那一行了，于是这个线程要访问b，又要去内存中找，增加了cache miss。此外多线程中，a那个线程多半是不会用到b的，于是平白做了cache位置的移动。

这个现象被称为假共享（false sharing），a和b并不是共享对象，但是由于他们靠的太近了，以至于在一个缓存行中，其中一个对象的更新，会强制另一个对象更新。

在多线程中，假共享可以通过缓存填充（cache padding）解决。缓存填充，就是在缓存中两个变量中间填充一些没有意义的数据，于是导致这两个变量不会处于同一个缓存行中，于是避免了假共享。

我们还是以统计图片像素为例，我们发现这种方法比直接用原子操作要快一些

struct bin{
    std::atomic<int> count; //4 bytes
    uint8_t padding[64 - sizeof(count)];    //60 bytes
};
//cache padding
std::vector<bin, tbb::cache_aligned_allocator<bin>> hist_p6(num_bins);
t0 = tbb::tick_count::now();
parallel_for(tbb::blocked_range<size_t>{0, image.size()},
             [&](const tbb::blocked_range<size_t>& r)
             {
               for(size_t i = r.begin(); i < r.end(); ++i)
               {
                 hist_p6[image[i]].count++;
               }
             }
            );

我们可以用C++特性来创建结构体：

struct bin{
    //C++17后，可以用std::hardware_destructive_interference_size替代64
    alignas(64) std::atomic<int> count;
};

代理

TBB的TBBmalloc库使用代理方法，可以实现在不同操作系统，不改变代码，只需要配置一些动态库、代理库、环境变量，就可以实现全局替换new、malloc等分配函数，这对跨平台真的很重要

Task调度

Chapter10

资料

Pro TBB

API Document

代码仓库

Pro-TBB

Pro TBB

概念

并发和并行

TBB基础

Mac上安装使用TBB

在Ubuntu上安装TBB

调用函数

快排示例

时刻查询

Flow Graph

循环

归约

求最大值

扫描

前缀和

可见性

parallel_for_each

前向替换

流水线

Flow Graphs

预热

数据流图

节点

function_node

join_node

链接

激活

等待

性能限制

依赖图

前向替换

PSTL

同步

写冲突

RMW

锁

原子操作

Thread Local Storage

ETS

combinable

parallel_reduce

并发容器

concurrent_hash_map

内存分配

缓存填充（对齐）

代理

Task调度

资料