七:衍射
内容概述
- 衍射(Diffraction),光在传播途中偏移直线传播,强度重新分布的过程
- 惠更斯-菲涅尔原理
- 定量分析衍射
- 统一衍射和直线传播
衍射
衍射是光在传播途中偏移直线传播,强度重新分布的过程
物体遮挡光线,就会产生阴影
在几何光学中,平行光只会被完全遮挡/完全不遮挡,因此阴影应该是清晰的
但现实中的平行光阴影是软阴影,其实就是发生了衍射
点、面光源的软阴影是由于光源由尺寸
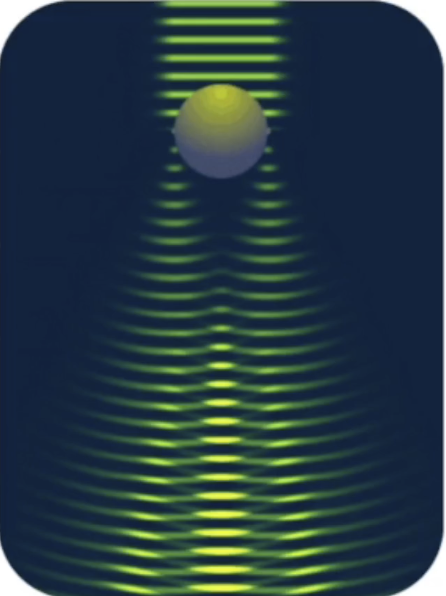
一组平行的波阵面通过小孔,会变成圆形

波长越长,越容易观测到衍射
- 小孔尺寸在波长的1000倍左右时衍射现象不明显
- 小孔尺寸在波长的10倍左右时衍射十分明显
- 小孔尺寸和波场相近时会发生散射
衍射的分类
- 菲尼尔衍射(近场衍射):光源和接收屏距离有限
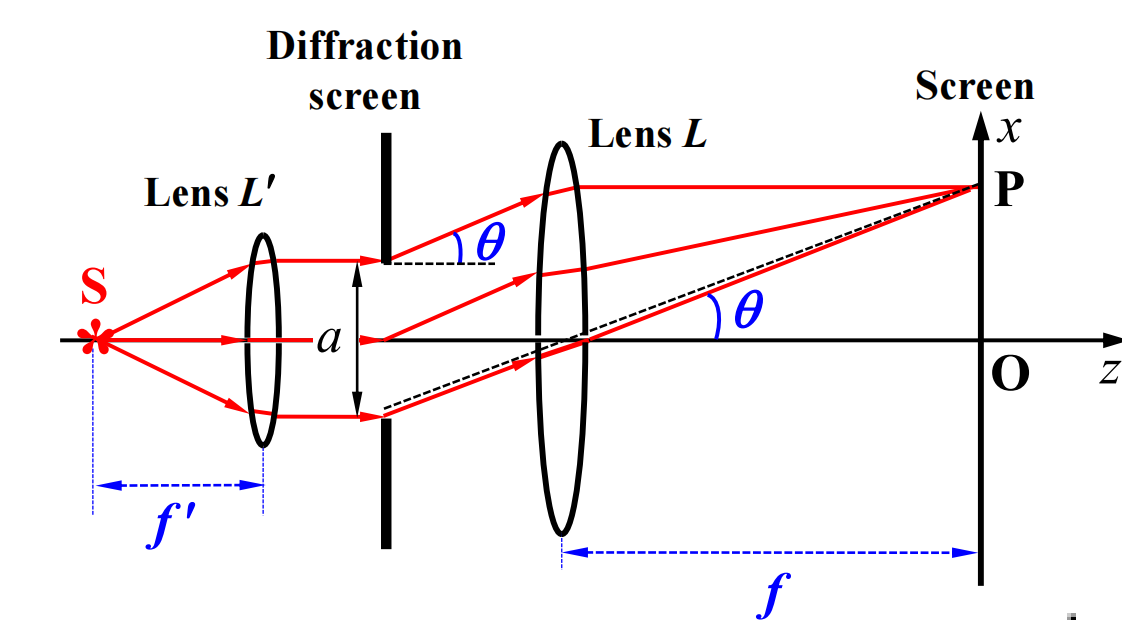
- 夫朗禾费衍射(远场衍射):光源和接收屏距离无限(也就是入射光是平行光)
夫朗禾费衍射需要用透镜将平行光汇聚

光栅衍射
多光束干涉和单缝衍射的混合
多光束干涉决定明条纹位置
$$
d\sin \theta=k\lambda
$$
缺级
$$
k=\frac{d}{a}k’
$$
干涉与衍射的关系
相同:
- 干涉和衍射都是相干叠加
不同:
- 干涉是离散点光源叠加求和,衍射是连续次波源叠加积分
- 干涉满足几何光学规律,衍射不满足几何光学规律
惠更斯-菲涅尔原理
惠更斯
惠更斯:波阵面上每一个点,本质上是一个球面次级小波的发射源,下一个波阵面实际上是这些球面的包络线(envelope)
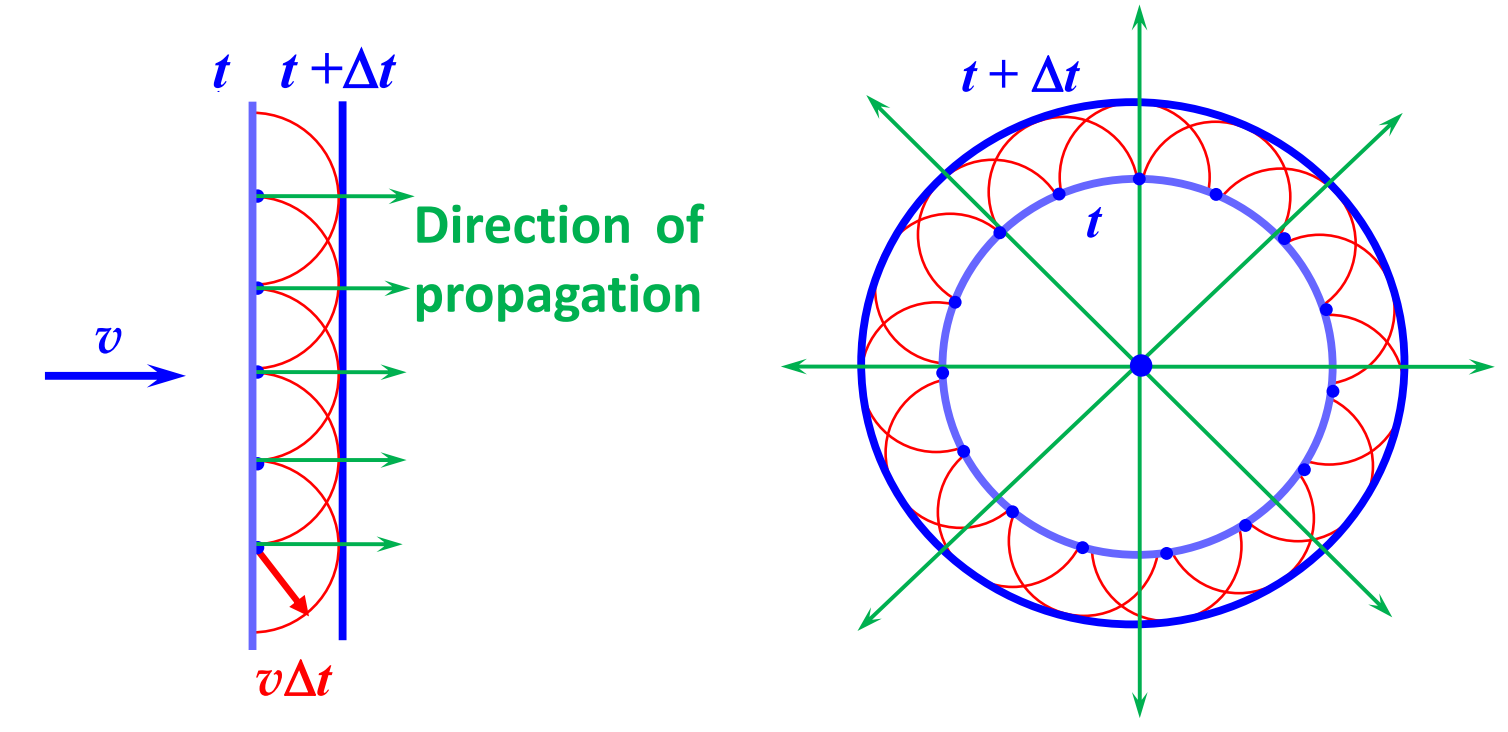
理论的作用
- 根据这个理论,给定一个波阵面,我们可以画出下一个波阵面
- 解释了光在各向同性介质中的传播原理
- 解释了反射和折射公式
局限性
- 无法区分光沿直线传播和发生衍射的条件
- 无法定量分析衍射强度
- 根据该理论,应该会有反转波
菲涅尔
菲涅尔修正了惠更斯的理论
- 波阵面上每一个(无阻塞)点都是球面波的发射源,频率与主波相同
- 不在波阵面上的点,都是由小波相干叠加得到的
衍射是无数干涉的叠加
倾斜因子
惠更斯的理论会应该会存在向后的波,菲涅尔引入了倾斜因子(Tilt factor)
$$
F(\theta_0, \theta)=\frac{1}{2}(\cos\theta_0+\cos \theta)
$$
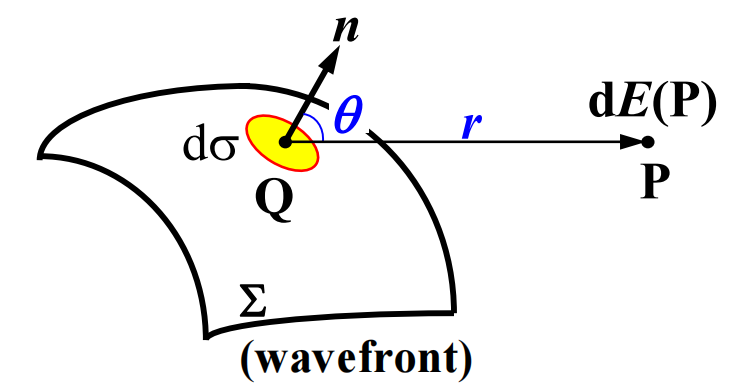
倾斜因子的引入使得向后的波强度为0,自然就不会出现反转波
不过倾斜因子的引入是纯经验,这也是菲涅尔理论的局限性
基尔霍夫积分定律
基尔霍夫在倾斜因子的基础上添加了一个常数K,提供了一个$-\pi/2$的相位差
$$
K=\frac{e^{-i\pi/2}}{\lambda}
$$
于是衍射积分公式转化为:
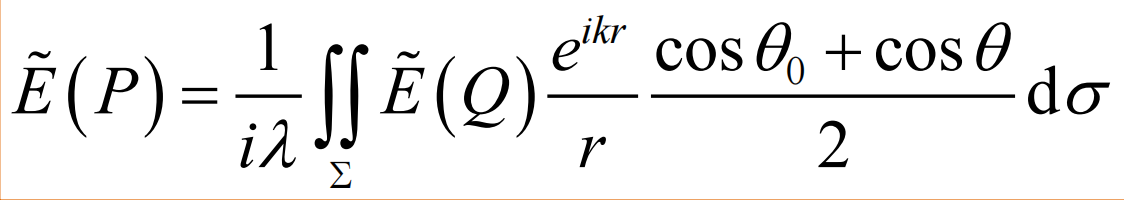
巴俾涅原理
两个互补的衍射屏叠加,效果等同于自由传播
半波带法
下图为单缝夫朗禾费衍射,计算方法为半波带法
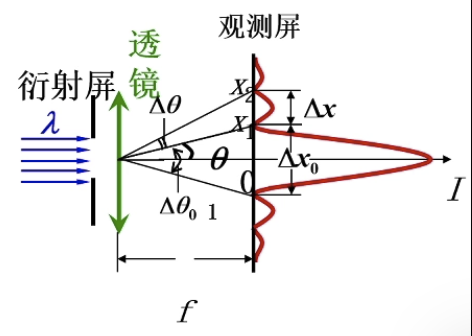
波带数
$$
\frac{a \sin \theta}{\lambda/2}
$$
- a是衍射屏孔径
暗纹位置(暗纹准确,明纹不准确)
$$
a \sin \theta = \pm k \lambda
$$
中央明纹宽度
$$
\Delta x_0=2f\frac{\lambda}{a}
$$
衍射图样
单缝衍射
圆孔衍射
圆孔衍射:亮暗相间的同心圆环,中心可能是暗也可能是亮的
中心强度与孔径明暗,与屏幕距离不敏感

Airy斑:中心圆斑
瑞丽判据:如果一个物点的Airy斑的边缘在另一个Airy斑中心上,那么这两个物点恰好可分辨
圆屏衍射
圆屏衍射:亮暗相间的同心圆环,但中心总是一个亮点
亮点与物体大小、屏幕距离都无关,这个亮点我们称为柏松亮斑

一个圆球的影子,中心居然会有一个亮点,衍射,很神奇吧
光栅衍射
菲涅尔波带片
根据菲尼尔衍射原理,将偶数个半波带遮挡住,就能得到菲涅尔波带片(就是对一个平整的圆形玻璃,将其表面部分图黑一个个同心圆环)

若一个波带片有20个半波带,遮挡偶数个半波带,轴上中心点的光强为
$$
A’=A_1+A_2+A_3+A_4+A_{19}\approx 10A_1=20A_0
$$
$$
I’=A’^2=400A_0^2=400I
$$
我们发现中心点的光强变强,因此菲涅尔波带片相当于透镜,可以汇聚光强
涂黑半径
$$
\rho_K=\sqrt{k}\rho_1
$$
- k取1,2,3…
成像公式
$$
\frac{1}{R}+\frac{1}{b}=\frac{1}{f}
$$
- R:点光源到波带片的距离
- b:波带片到汇聚点到距离
波带片与透镜
- 相同
- 都能汇聚能量
- 不同
- 透镜只有一个汇聚点,波带片有多个实汇聚点和虚汇聚点
- 透镜满足等光程性,波带片相邻波带片间有一个波长的光程差
- 波带片面积大、轻便、可折叠



