三:电磁波
内容概述
- 横波的性质(nature),强度(intensity),能量流动(energyflow)
- 偏振态(Polarization states),琼斯矩阵(Jones matrix/vector)
- 吸收(Absorption),色散(dispersion),折射率(refractive index)
- 微小粒子导致的散射(Scattering)
波
构成波的条件:
- 波源
- 介质
- 能量来源
波的性质:
- 时间周期性
- 空间周期性
- 能量传播
波的分类
- 标量波
- 矢量波
光的基本性质
-
光是电磁波
-
可见光的波长在400nm~760nm
- 在做干涉衍射计算时,经常去白光的平均波长550nm
-
人眼对550nm的黄绿光最敏感
-
单色光(Monochromatic light),指仅有一种波长的光,仅存在于理论中
光速
光在真空(vacuum)中的速度(简称光速,用c表示)为
$$
c=\frac{1}{\sqrt{\varepsilon_0 \mu_0}}=2.997 924 58 \times10^8 m/ s
$$
光在介质(medium)中的速度(也叫做相速度,用v表示)为
$$
v=\frac{1}{\sqrt{\varepsilon_0 \varepsilon_r\mu_0\mu_r}}=\frac{c}{\sqrt{\varepsilon_r \mu_r}}
$$
很显然光在介质中的速度比在真空中慢,我们用折射率(Refractive index,用n表示)来描述这一性质
$$
n=\frac{c}{v}
$$
光穿过线性介质(linear medium)时,其频率不会发生改变
光的波长(用$\lambda$表示)
$$
\lambda=\frac{c}{v}
$$
波粒二象性
波
如果光是波,那么光应该有波的性质:
$$
\mathbf{k}=\frac{2\pi}{\lambda}\hat{\mathbf{k}}
$$
$$
v=\frac{\lambda}{T}=\lambda \nu
$$
$$
\omega=2\pi \nu =\frac{2\pi}{T}=\frac{2\pi}{\lambda}v=kv=k_0c
$$
- 波长(wavelength,用$\lambda$表示)
- 波向量(wave vector,用$\mathbf{k}$表示)
- 频率(frequency,用$\nu$表示)
- 周期(temporal period,用$T$表示)
- 角频率(angular frequency,用$\omega$表示)
- 速度(velocity,用$v$表示)
光是电磁波,其电矢量和磁矢量在做简谐振动,一般情况下,我们只讨论电场强度的变化
粒
如果光是粒子,那么光应该有粒子的性质:
$$
E=h\nu=\hbar \omega
$$
$$
\mathbf{p}=\hbar \mathbf{k}=\frac{h}{\lambda}\hat{\mathbf{k}}
$$
- 能量(Energy,用$E$表示)
- 动量(Momentum,用$\mathbf{p}$表示)
- 普朗克常量(Plank constant,用$h$表示,$h=6.626\times 10^{-34}\mathrm{J}\cdot\mathrm{s}$
- 约化普朗克常量(用$\hbar$表示)
波粒二象性
光具有波粒二象性(Wave-particle duality),光在传播过程中体现出明显的波性,在光与物质交互(light-matter interaction)中粒性更明显
光子与电子
不同之处
| 电子 | 光子 | |
|---|---|---|
| 静止质量(Rest mass) | $m_0$ | 0 |
| 运动质量(Motion mass) | $m$ | $hv/c^2$ |
| 运动速度(Motion velocity) | $<c$ | $c$ |
| 自旋(Spin) | 1/2 | 1 |
| 分布定律 | 费力(Fermion) | 玻色(Boson) |
相同之处
- 满足波粒二象性
向量波与标量波
向量波(Vector wave),波函数是向量的波,比如电磁波(EM wave)
标量波(Scalar wave),波函数是标量的波,比如声波(Acoustic wave)
光波(Lightwaves)是一种向量波,但为了方便,我们在讨论干涉衍射时,会认为光是标量波,仅仅在讨论偏振时,才认为光是向量波
电磁波
物理量
- 电场强度(用$\mathrm{E}$表示):单位电荷在电场中受到的力
- 磁场强度(用$\mathrm{H}$表示):通电导线周围有磁场,其强度与电流大小、距离远近有强度(但实际被后世推翻,无实际意义)
- 电场通量密度(用$\mathrm{D}$表示):单位面积的电场通量
- 磁场通量/感应密度(用$\mathrm{B}$表示):经过一个曲面的磁力线的数量
电磁学三定律
库伦定律,真空中两个静止的点电荷间作用力满足
$$
F=k\frac{q_1q_2}{r^2}
$$
- 静电力常量($k=9.0\times 10^9 \mathrm{N} \cdot\mathrm{m^2}/\mathrm{C^2}$)
安培环路定律(Ampère’s Circuital Law),也叫右手螺旋定则,载流导线能生磁
法拉第电磁感应定律(Faraday’s Induction Law),磁场变化能产生电场,感应电动势大小与磁通量变化率成正比,电场方向符合楞次定律(由于磁通量的改变而产生的感应电流,其方向为抗拒磁通量改变的方向)
麦克斯韦方程
真空中麦克斯韦方程:
法拉第
$$
\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}
$$
安培
$$
\nabla \times \mathbf{B}=\mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}
$$
- 真空磁导率(也称为磁常数,用$\mu_0$表示,$\mu_0=4\pi \times 10^{-7}\mathrm{H}/\mathrm{m}$)
- 真空电容率(也称为电常数,用$\varepsilon_0$表示,$\varepsilon_0=8.854…\times10^{-12}\mathrm{F}/\mathrm{m}$)
高斯电场
$$
\nabla \cdot \mathbf{E}=0
$$
高斯磁场
$$
\nabla \cdot \mathbf{B}=0
$$
自由空间的波动方程(wave equations,由麦克斯韦方程推出):
$$
\nabla^2\mathbf{E}=\mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2}
$$
$$
\nabla^2\mathbf{B}=\mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{B}}{\partial t^2}
$$
平面波
三维的电磁波很难分析,我们可以分解变量,将其转化为两个垂直的平面波
平面波(Plane waves):传播时波面在一个平面的电磁波
平面波的电场方向和磁场方向,与波矢方向垂直,如图,$\mathbf{k}$为波矢方向(推导过程略),从这里也能看出,平面波是横波,方向满足右手定则
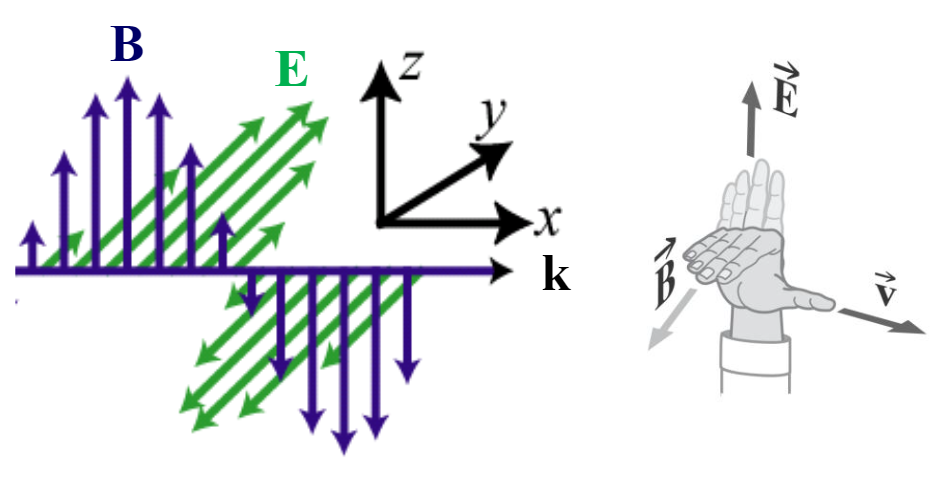
平面波的磁感应强度B和电场强度E的比值等于波速
$$
\frac{|E|}{|B|}=\sqrt{\frac{1}{\mu \varepsilon}}=v
$$
电场强度和磁场强度的关系为(注意,这里不是磁感应强度)
$$
\sqrt{\varepsilon_0 \varepsilon_r}|\mathrm{E}|=\sqrt{\mu_0\mu_r}|\mathrm{H}|
$$
自由空间阻抗(单位和电阻相同,用$Z_0$表示)
$$
Z_0=\sqrt{\frac{\mu_0}{\varepsilon_0}}=376.73\Omega
$$
波能传递能量,我们引入坡印廷向量(Poynting vector,用$\mathrm{S}$来表示)来描述能量流动,其方向为电磁能传递方向,大小为能流密度(单位面积的能量传输速率)
$$
\mathrm{S}=\mathrm{E}\times \mathrm{H}
$$
平面波$\mathrm{E}\times \mathrm{H} // \mathrm{k}$
傍轴条件
当$\rho \ll z,r \approx z$
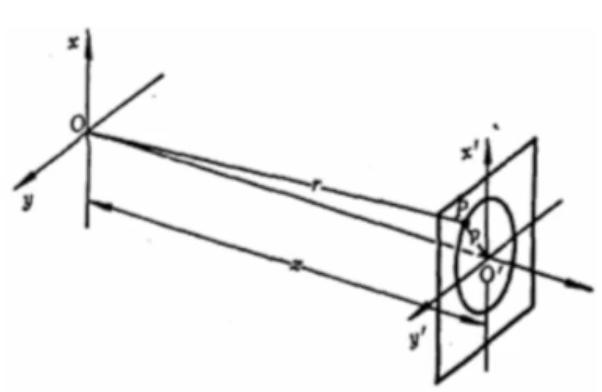
远场条件
辐照度
电磁波的辐照度(Irradiance,用$\mathrm{I}$表示,也称为Intensity),是坡印廷向量在时间上的平均值
$$
\mathrm{I}=\left< \mathrm{S} \right>=\frac{nc\varepsilon_0}{2}\mathrm{E_0}^2
$$
- $c$是真空中光速
- $\mathrm{E_0}$是电磁波电场强度的振幅(电场强度是一个三角周期函数)
从这里可以看出,辐照度与$\mathrm{E_0}$的平方成正比
偏振
偏振(Polarization):光矢量在垂直于传播方向的平面上的震动状态,我们这里提的是电场强度$\mathrm{E}$的震动
-
根据是否发生偏振
- 不偏振光(Unpolarizedlight)
- 完全偏振光(Completely polarized light)
- 部分偏振光(Partially polarized light)
-
根据向量$\mathrm{E}$的终点(endpoint)轨迹
- 线偏振(Linearly polarized light)
- 圆偏振(Circularly polarized light)
- 椭圆偏振(Elliptically polarized light)
若光线沿着z轴传播,其方程满足
$$
(\frac{E_x}{E_{0x}})^2+(\frac{E_y}{E_{0y}})^2-2(\frac{E_x}{E_{0x}})(\frac{E_y}{E_{0y}})\cos \delta = \sin ^2 \delta
$$
线偏振
当$\delta=2m\pi$时,方程变为
$$
(\frac{E_x}{E_{0x}})^2+(\frac{E_y}{E_{0y}})^2-2(\frac{E_x}{E_{0x}})(\frac{E_y}{E_{0y}}) = 0 \
(\frac{E_x}{E_{0x}}-\frac{E_y}{E_{0y}})^2=0
$$
于是得到线偏振的方程(一三象限)
$$
\frac{E_x}{E_{0x}}=\frac{E_y}{E_{0y}} \equiv \cot \alpha
$$
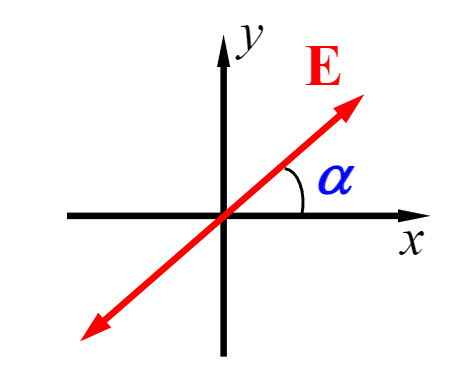
同理,当$\delta=2(m+1)\pi$时,方程等于(二四象限)
$$
\frac{E_x}{E_{0x}}=-\frac{E_y}{E_{0y}}
$$
用虚数将两个方程合并,得到
$$
\frac{E_x}{E_{y}}=\frac{E_{0x}}{E_{0y}}e^{\mathrm{i}m’\pi}
$$
- 当$m’$为偶数(0 or even)时,一三象限
- 当$m’$为奇数(odd)时,二四象限
椭圆偏振与圆偏振
当$\delta=(2m+1)\frac{\pi}{2}$时,方程变为
$$
(\frac{E_x}{E_{0x}})^2+(\frac{E_y}{E_{0y}})^2=1
$$
这是一个椭圆方程,我们称之为椭圆偏振
倘若$E_{0x}=E_{0y}=E_{0}$,方程退化为
$$
E_x^2+E_y^2=E_0^2
$$
我们称之为圆偏振
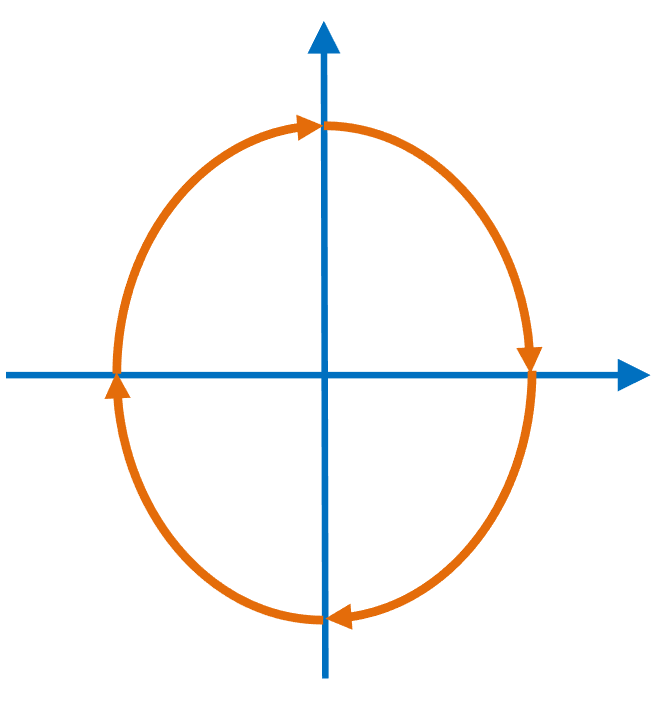
-
当$\delta=\pi / 2$时,y轴驱动x轴移动,此时为顺时针,称为RCP
-
当$\delta=-\pi / 2$时,x轴驱动y轴移动,此时为逆时针,称为LCP
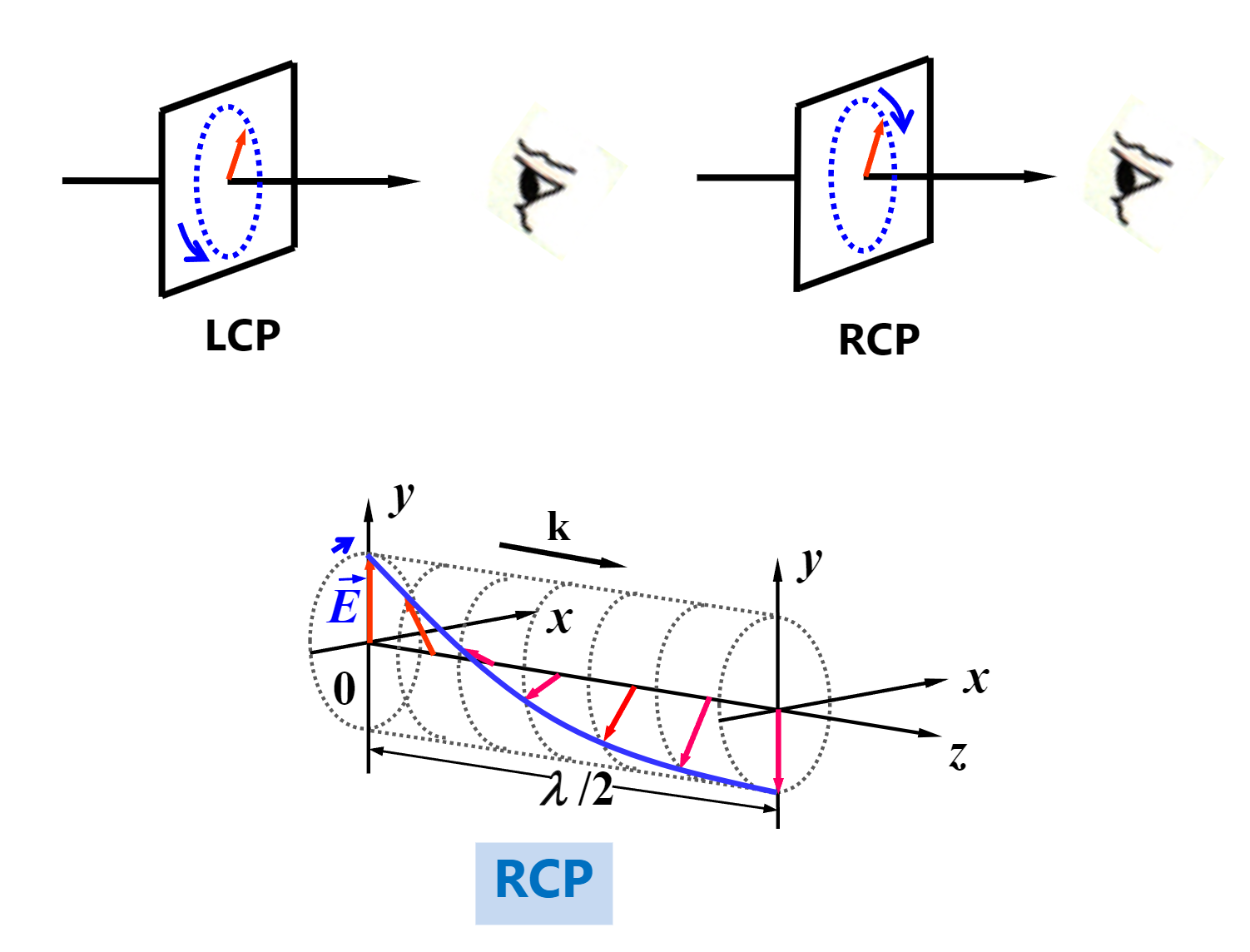
琼斯矢量
将偏振光的状态以向量的形式写出,方便运算(只适合完全极化光)
$$
\mathrm{E}=\left[
\begin{array}{c}
E_x(t)\
E_y(t)\
\end{array}
\right]
$$
琼斯向量左乘一个2x2矩阵,可以得到一个新的琼斯向量,这个矩阵被称为琼斯矩阵
偏振度
偏振度(Degree of polarization,用$P$表示):用来衡量偏振程度的物理量
$$
P=\frac{I_p}{I_t}=\frac{I_p}{I_p+I_n}
$$
- $I_p$:完全偏振光部分的辐照度
- $I_n$:不偏振光部分(自然光)的辐照度
吸收
兰伯特定律
兰伯特定律(Lambert law):光在气体介质中传播,光强(intensity)随着传播深度增加而递减,满足
$$
I=I_0 e^{-\alpha x}
$$
- 吸收系数(用$\alpha$表示)
- 传播深度(用$x$表示)
贝尔定律
贝尔定律(Beer law):光在溶剂中传播,光强满足
$$
I=I_0 e^{-ACL}
$$
- 浓度(用$C$表示)
- 常数$A$,与溶质性质有关,与浓度无关
该公式满足有两个条件
- 溶液浓度不能过高,以免出现分子间作用力(这也能解释为什么常数$A$为什么和浓度无关,因为浓度一高,公式就不成立了)
- 光强不能过高
色散
色散(Dispersion):光波的相速度随着频率的改变而改变的现象
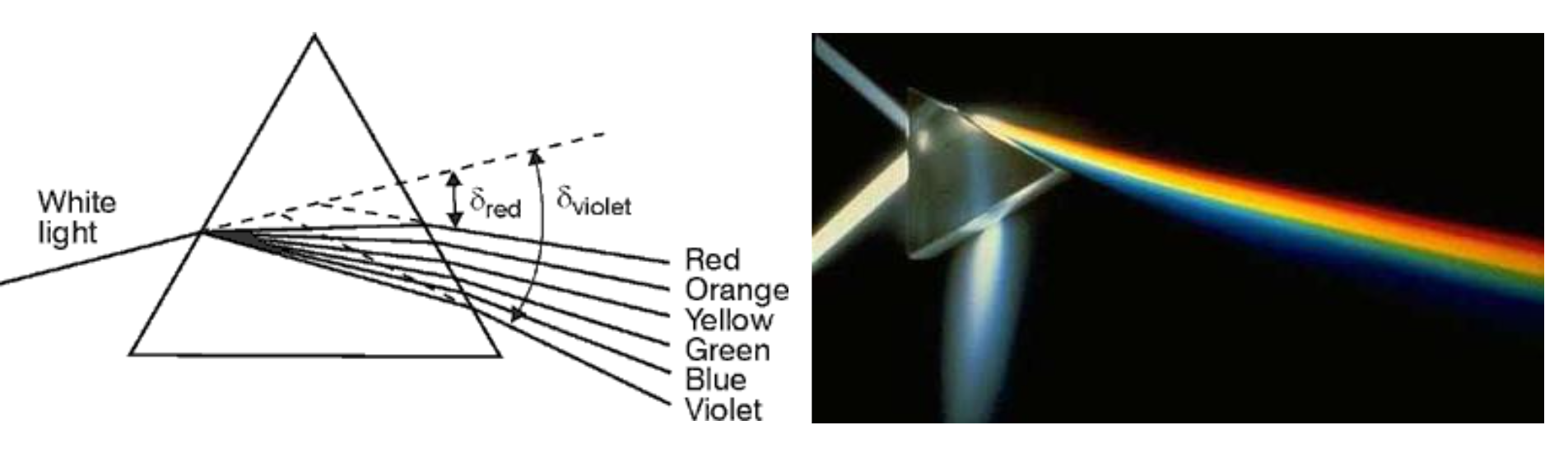
正常色散(Normal dispersion):折射率随着波长的增加而减小
柯西公式:
$$
n=A+B/\lambda^2+C/\lambda^4
$$
反常色散(Anomalous dispersion):折射率随着波长的增加而增加
反常色散通常发生在吸收带(absorption band)附近,反常色散并不是异常的,叫这个名字只是历史问题
洛伦兹震荡模型
洛伦兹震荡模型(Lorentz oscillator model):在一个尺寸为$\Delta V$的空间内有一个电子(电荷量为$1.6\times10^{-19}C$),在光的电场作用下,让该电子相对于稳定位置偏离x
偏振度(单位体积电偶极矩的振幅,用$P$表示)写作
$$
P=\frac{1}{\Delta V}ex=n_0ex
$$
- 电荷密度(density of charge,用$n_0$表示)
- $x$是电子的运动方程,如下
$$
x(\omega)=-\frac{eE(\omega)}{m_0}\frac{1}{\omega^2+\mathrm{i}\omega \gamma-\omega_0^2}
$$
将$x$带入,得到
$$
P=-\frac{n_0e^2}{m_0}\frac{1}{\omega^2+\mathrm{i}\omega \gamma-\omega_0^2}E(\omega)
\equiv \varepsilon_0 \chi(\omega)E(\omega)
$$
根据定义
$$
\varepsilon=\varepsilon_0[1+\chi(\omega)]
$$
带入得
$$
n^2=\varepsilon/\varepsilon_0=1-\frac{n_0e^2}{m_0}\frac{1}{\omega^2+\mathrm{i}\omega \gamma-\omega_0^2}
$$
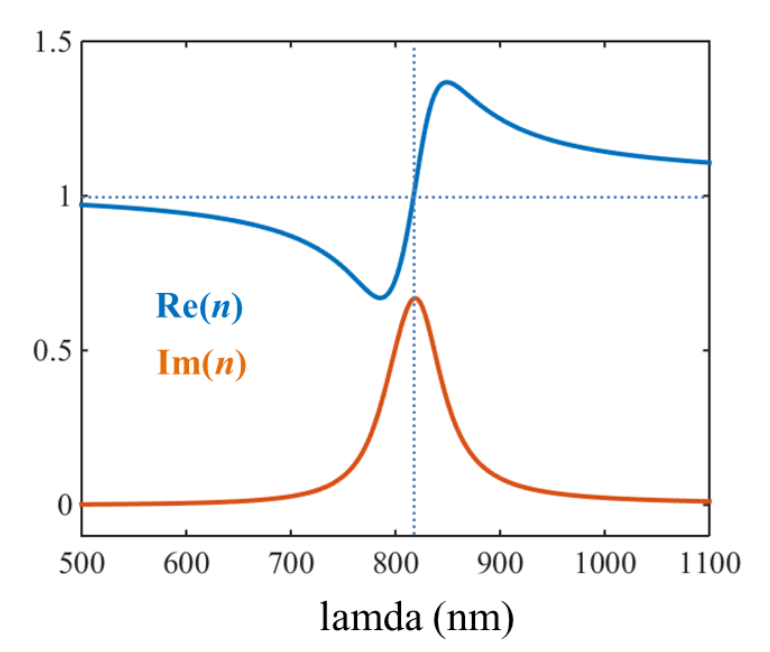
如图,洛伦兹模型解释了为什么在靠近吸收带时,会发生反常色散
组速度
在介质中不同波长的光速度不同,红光波长大,跑的更快
那么如果一个光,包含了多种波长的光,我们用组速度(Group velocity,用$v_g$表示)来描述其速度
$$
v_g=\frac{\mathrm{d}\omega}{\mathrm{d}k}
$$
散射
一般我们在讨论光在介质中传播,认为是没有损失的,但实际上光在介质中传播是存在吸收的
吸收:光强度随着穿进介质深度而减弱的现象
原因:
- 光能转化为其他能,比如热量、化学能、电能
- 发生散射,光向四面八方传播(丁达尔效应)
瑞丽散射
瑞丽散射(Rayleigh scattering):光在细小粒子间散射
$$
I_{scat}\propto 1/\lambda^4
$$
$$
I_{\theta}\propto I_{\pi/2}(1+\cos^2 \theta)
$$
米氏散射
米氏散射(Mie scattering):光在大型粒子内部散射



