抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

Reuben Sun

主页

图形

引擎

AI

编程

数学

光学

DCC

游戏

光学：干涉

optics

发布于：2023年2月25日

六：干涉

内容概述

  • 干涉（Interference），光的叠加不满足线性叠加，证明了光的波性
  • 干涉条件
  • 干涉方法与装置
  • 干涉仪

干涉

干涉让光学从线性光学变成非线性光学

线性光学

在几何光学中，我们认为光是独立传播的

光是一种横波，光在介质中传播会引起介质粒子振动，若独立传播成立，那么两束光的交叉区域，粒子的振动是两个振动的叠加，这就是叠加原理

光的叠加实际上是介质的性质（因为描述的是介质粒子振动的叠加）

  • 线性介质：在该介质中，波满足叠加原理
  • 非线性介质：在该介质中，波不满足叠加原理

违反叠加原理的介质是非线性介质，现象是非线性现象，学科是非线性光学

此外，叠加原理只有在低强度光下才成立，因此激光发明后，非线性光学才蓬勃发展

复振幅叠加法

求解相干光强有三种方法，实际分析时通常使用复振幅法

  • 三角函数法：波可以由三角函数表示，对三角函数做恒等变化，即可求相干光强
  • 矢量图解法
  • 复振幅法

首先将三角函数表示为复振幅
$$
\tilde{\mathbf{E}_i}=\mathbf{A}_i e^{i\varphi i}
$$
复振幅的叠加
$$
\tilde{\mathbf{E}}=\sum{i=1}^n\tilde{\mathbf{E}_i}
$$
合光强
$$
I = \tilde{\mathbf{E}}\cdot \tilde{\mathbf{E}}^*
$$

相干叠加

现在有两个相同频率（frequency）相同偏振（polarization）的光波，下面是他们电场强度随时间的变化（用复数表示三角函数）
$$
\mathbf{E_1}=\mathbf{A_1} e^{i(kr_1-\omega t+\varphi _{01})}
$$

$$
\mathbf{E_2}=\mathbf{A_2} e^{i(kr_2-\omega t+\varphi _{02})}
$$

他们相交于点P，根据叠加原理，P点点电场强度为
$$
\mathbf{E}=\mathbf{E_1}+\mathbf{E_2}=[\mathbf{A_1}e^{i(kr_1+\varphi_{01})} + \mathbf{A_2}e^{i(kr_2+\varphi_{02})}]e^{-i\omega t}
$$
显然，振幅为
$$
\tilde{\mathbf{E}}=\mathbf{A_1}e^{i(kr_1+\varphi_{01})} + \mathbf{A_2}e^{i(kr_2+\varphi_{02})}
$$
由于光过于高频，我们没法实时进行光电场强度的检测，于是我们使用光强（intensity，$I$）来进行推导

$$
I \propto \tilde{\mathbf{E}}\cdot \tilde{\mathbf{E}}^*=\mathbf{A_1}^2+\mathbf{A_2}^2+2\mathbf{A_1A_2}\cos(kr_1-kr_2+\varphi_{01}-\varphi_{02})
$$

$$
I = I_1+ I_2 + 2\sqrt{I_1I_2}\cos \delta
$$

$$
\delta=kr_1-kr_2+\varphi_{01}-\varphi_{02}
$$

我们发现，两个光波进行叠加，光强不只是简单叠加，还有一个尾巴，这个尾巴就是干涉

干涉：因波的叠加引起强度重新分布的现象

并且我们发现：

  • 干涉强度与时间无关，与空间位置有关，且保持不变

  • 当$\delta=2m\pi$，干涉强度最大，我们称之为构造干涉（constructive interference）

$$
I=(\mathbf{A_1}+\mathbf{A_2})^2
$$

  • 当$\delta=(2m+1)\pi$，干涉强度最小，我们称之为相消干涉（destructive interference）

$$
I=(\mathbf{A_1}-\mathbf{A_2})^2
$$

非相干叠加

一般而言，两个光频率和偏振不一样，经过推导
$$
I_{12}=2\mathbf{A_1}\cdot \mathbf{A_2} \cos [(\omega_2 - \omega_1)t + \theta_1 - \theta_2]
$$
我们到处干涉强度为0的条件

  • 两个光频率不同，$\cos[…]$的均值为0
  • 两个光光矢量垂直，$\mathbf{A_1}\cdot \mathbf{A_2}=0$
  • 两个光夹角（相位差）迅速且无序变化，$\cos[…]$的均值为0

干涉条件

因此我们总结出发生干涉的条件

  • 频率相同
  • 相同的平行分量
  • 固定的相位差

如果不满足干涉条件，那么平均下来
$$
I=I_1+I_2
$$

杨氏干涉

普通光源：普通光源的发光单位为原子、分子，不同原子间的发光是独立的，他们的频率、偏振、相位都是不同的，因此他们的光是不会发生干涉的

有干涉条件我们可以得出两种获得干涉光的方法：

  • 分波前法（杨氏干涉）
  • 分振幅法（薄膜等厚干涉）

使用杨氏干涉实验、菲涅尔双棱镜、劳埃德镜可以将普通光源变成干涉光

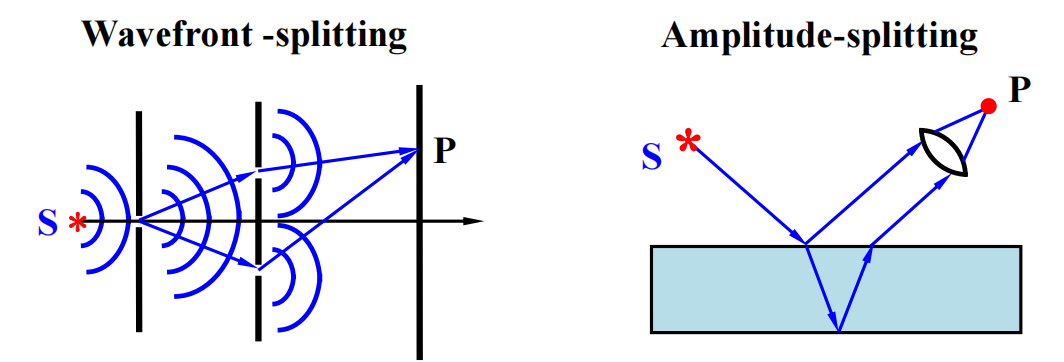
普通光源相干光

杨氏干涉，两束光的出相相同，因此干涉光的相位差只取决于光程差
$$
\Delta \varphi= \frac{2\pi }{\lambda}\Delta OPL=k\delta
$$

  • k：波数，$k=\frac{2\pi}{\lambda}$
  • $\delta$：光程差

衬比度

衬比度，也可以叫做可见度

干涉条纹的衬比度（constrast）定义为
$$
\gamma = \frac{I_\max-I_\min}{I_\max + I_\min}
$$
用于描述条纹的反差程度，当可见性为1时最清晰，当为0时完全不可分辨

杨氏双缝干涉实验

杨氏实验是通过两个点波光源进行干涉实验的典型

如果光是一种波，那么光在传播过程中应该会有波前（传播最靠前的波阵面），提取一个波前，并将其分为两部分，就能得到两个相干光

现在有一个非常窄的单色光源，经过两个带缝平面，会生成两个相干光，进而发生衍射现象，在平面留下明暗条纹

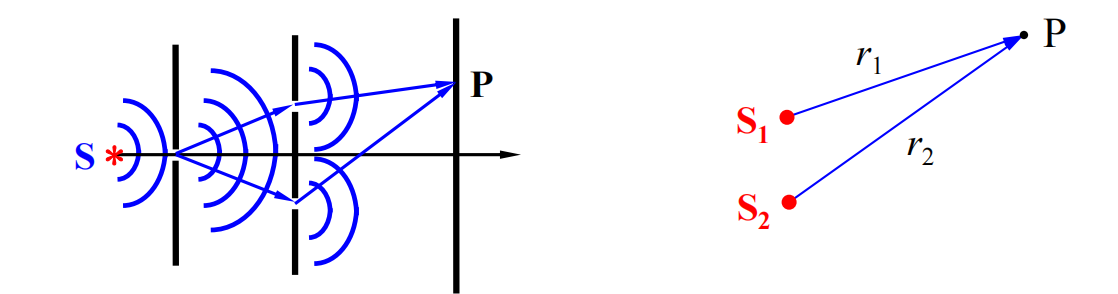
杨氏双缝干涉

$$
I=A^2=4I_1\cos^2\frac{\pi \Delta}{\lambda}
$$

  • 若$\Delta=m\lambda, I=I_{max}=4I_1$，呈现亮条纹
  • 若$\Delta=(2m-1)\lambda/2, I=I_{min}=0$，呈现暗条纹

杨氏干涉实验的衬比度为
$$
\gamma = \frac{2(A_1/A_2)}{1+(A_1/A_2)^2}
$$
杨氏干涉

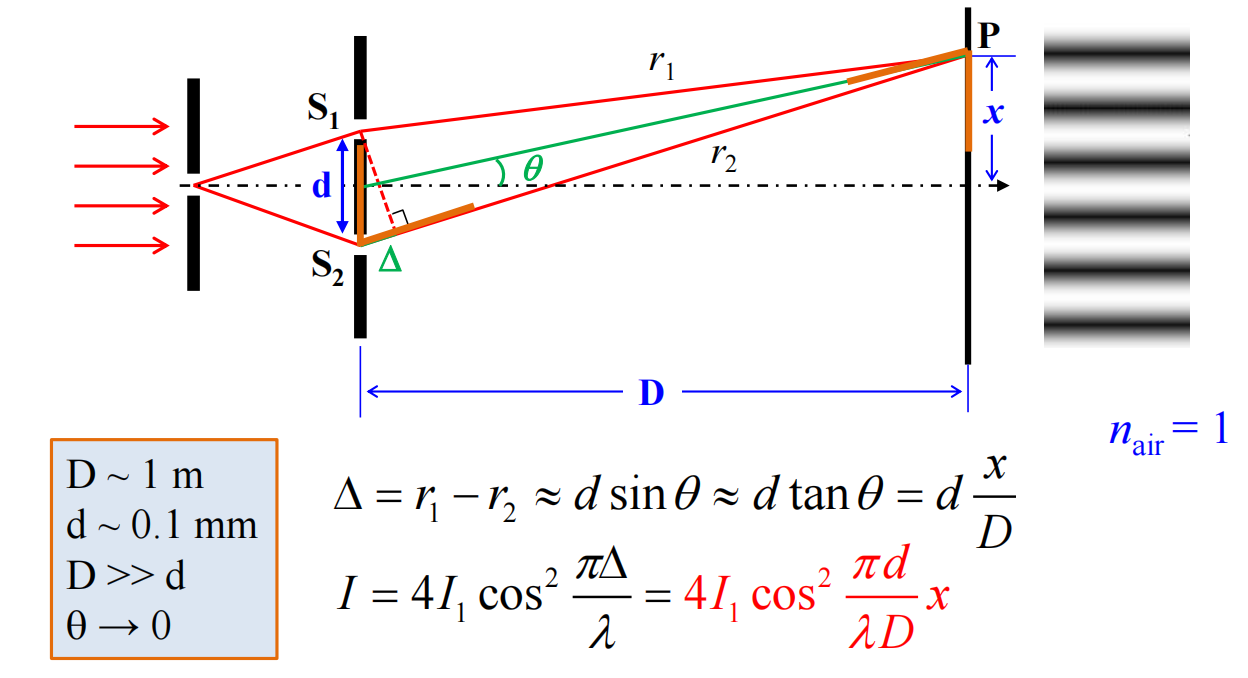
当间距不大时，角度比较小，缝间距是相同的，间距为
$$
\Delta x=\frac{D}{d}\lambda
$$

判断一点的暗亮

看上图

在杨氏干涉实验中，给定$d,D,x$，判断点在明条纹中还是暗条纹中

核心思想就是：判断光程差是半波长的偶数倍还是奇数倍，偶数为明条纹，基数为暗条纹

  1. 以P点为圆心，$S_1P$为半径画一个圆，圆和$S_2P$相交于点$S’$，那么$S_2S’$就是光程差
  2. 不过$S_2S’$很难求，于是我们进行近似，我们从$S_1$出发做$S_2P$的垂线，垂足可以近似为点$S’$
  3. 我们知道斜边长度为d，只要知道$\angle S_2S_1S’$，就能求出光程差
  4. 不过$\angle S_2S_1S’$还是太难求了，我们用角$\theta$来近似
  5. $\sin \theta \approx \tan \theta = x/D$
  6. 有了光程差，就能知道这是几个波长，是明是暗

可见条纹的最大级数

$$
j_\max= d/\lambda
$$

求P点光强

$$
I=A_1^2+A_2^2+2A_1A_2\cos \Delta\varphi
$$

$$
\Delta \varphi = k \cdot \delta
$$

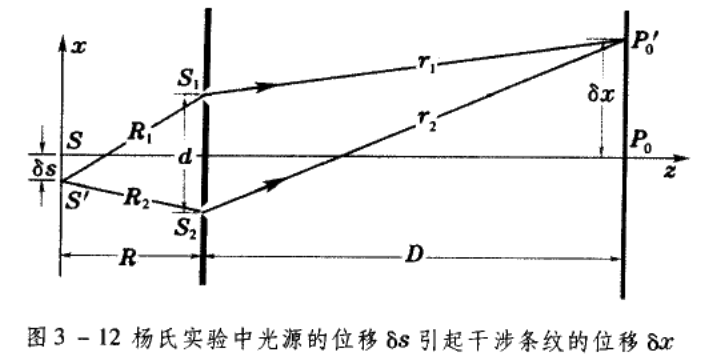
干涉条纹的移动

我们不仅观测到明暗条纹，还观测到条纹的移动和变化

  • 移动光源，对于屏幕上一点，求多少个条纹经过该点

    • 对于屏幕上点P，经过点P的条纹数取决于两条相干光线的光程差（OPL）
    • 当光程差增减一个$\lambda$时，就会经过一条条纹

  • 移动光源，对于特定的一个条纹，求其移动了多长距离

    • 杨氏双缝中

$$
\delta x = -\frac{D}{R}\delta s
$$

条纹移动

其他干涉仪器

本质都是杨氏双缝干涉，条纹间距都满足
$$
\Delta x=\frac{D}{d}\lambda
$$

这些干涉仪器相比起杨氏干涉，不使用狭缝过滤光，因此光线强度更高

菲涅尔双平面镜

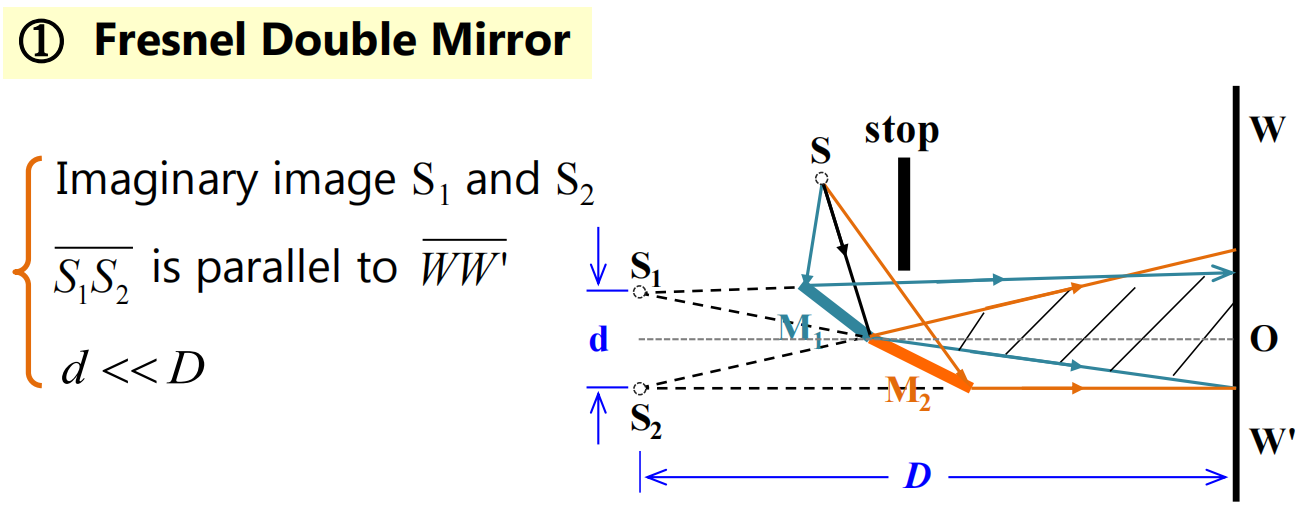
菲尼尔双平面镜

劳埃德镜

劳埃德镜

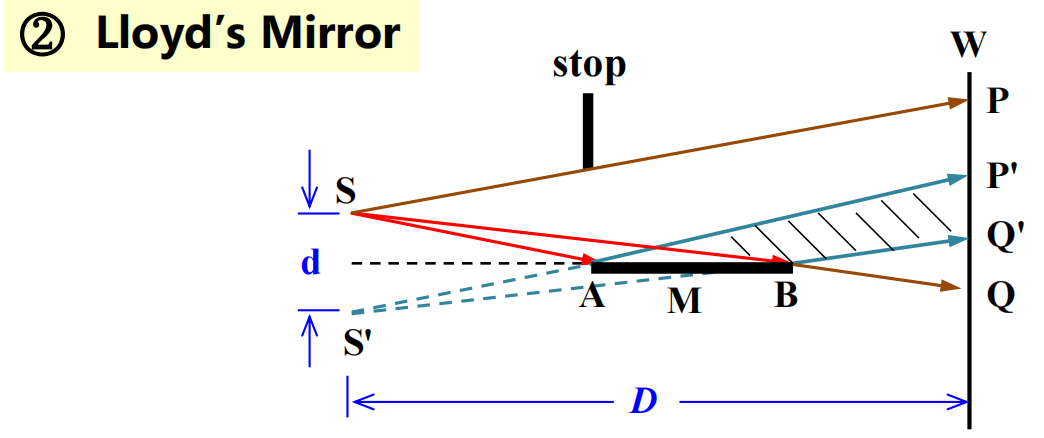
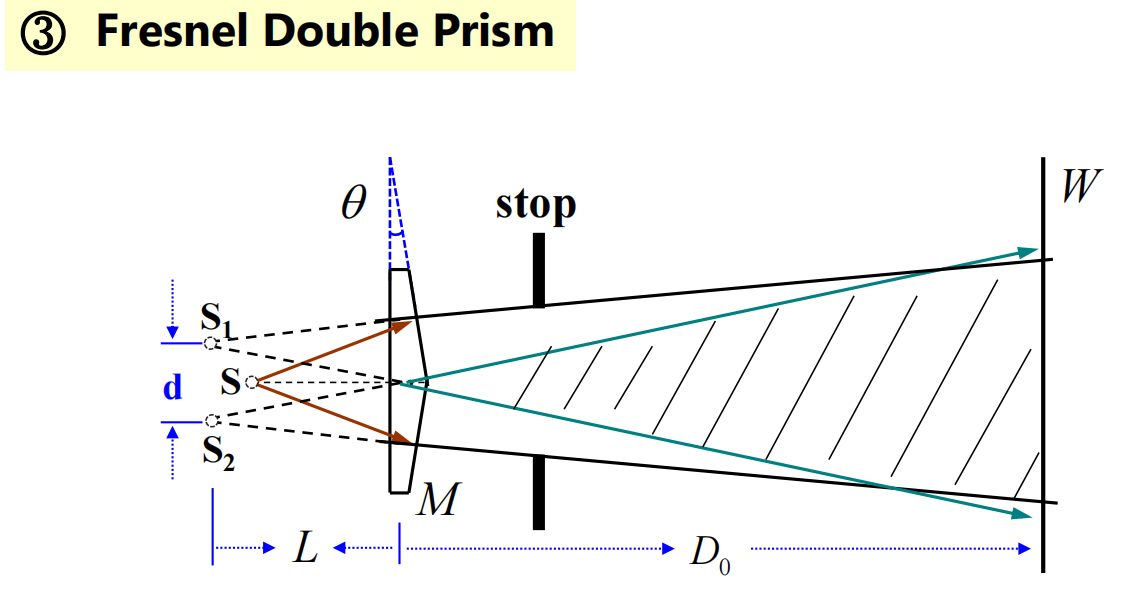
菲涅尔双棱镜

菲涅尔双棱镜

彩色光杨氏双缝

如果传入的是白光，条纹将为彩色

杨氏干涉彩色条纹

时空相干性

现实中的普通光源的发光单元为原子、分子，靠自发辐射发光（激光光源靠受激辐射），这是一个随机过程，产生的光是随机、无规律、不相干的。看起来我们无法用普通光源做干涉实验，但实际上杨氏双缝是可以使用普通光源的，因为杨氏双缝中两个光都是由同一束光分割而成的

尽管普通光源的相位随机，但是杨氏双缝两束光的相位差与原光源相位无关，仅与空间位置有关

不过，光源的尺寸和光谱尺寸仍然会对杨氏干涉产生影响

在杨氏干涉中，我们使用了很窄的单色光源，然而现实中光源总是有尺寸，其颜色也不是单色而是光谱中一小段

空间相干性：光源尺寸对干涉强度的影响

时间相干性：光谱尺寸对干涉强度的影响（也就是说光不是真的纯色）

空间相干性

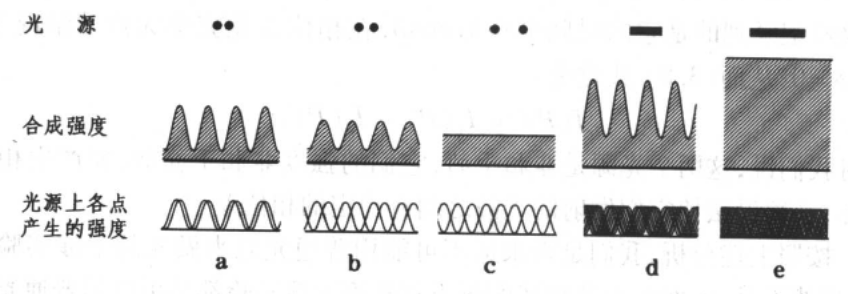
任何光源都有一定的宽度，我们将其视为多个不相干的点光源排布，屏幕上的总强度为各个光源的干涉条纹的线性叠加

我们发现沿着x轴方向的长度会让条纹模糊

沿着y轴方向的长度会让亮纹和亮纹重叠，于是条纹更清晰

我们在做杨氏双缝时常常使用平行于y轴方向的光

光源宽度 空间相干性

时间相干性

现实中光不是纯色光，光的波长不同，干涉条纹长度不同，于是不同波长的干涉条纹就会发生重叠，进而降低条纹的衬比度

薄膜干涉

薄膜（film）一种透明介质，将空间划分三个折射率不同的区域，其中中间的区域不能过厚

薄膜干涉（Thin film interference）：光在薄膜表面发生反射和折射，下表面的反射光和上表面的折射光发生干涉

比如彩色太阳眼镜和阳光下的七彩肥皂泡

光线在射向薄膜后会发生反射和透射，透射光可能会再次反射透射，返回薄膜表面，进而和入射光相遇，发生干涉

  • 等厚干涉：发散的入射光（点光）和透射光干涉，干涉发生在薄膜表面
  • 等倾干涉：平行的透射光干涉，干涉发生在无穷远，需要用透镜汇聚，形状为同心条纹

特别注意！等厚和等倾是指的条纹间距，而不是薄膜形状，等厚的条纹需要上下不平行的薄膜

等厚度干涉

薄膜干涉

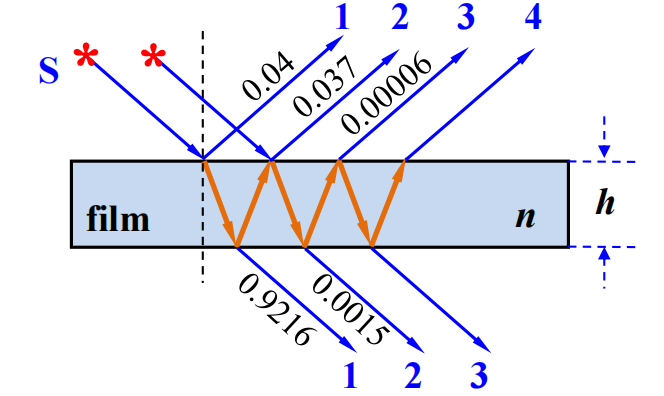
等厚干涉发生在薄膜表面

厚度不均匀的薄膜发生的干涉，入射光为平行光，决定条纹间距的是因厚度不均带来的光程差
$$
\delta = 2nh\sqrt{n^2-n_0^2\sin^2 i_1} +\lambda/2
$$

  • $i$是折射角

常见的等厚干涉有

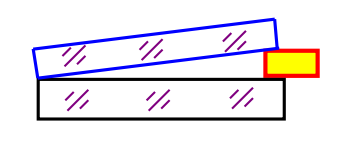
  • 劈尖：光线垂直入射
    • 角度越大，条纹数量越多
    • 折射率越大，条纹间距越大

空气劈尖

  • 牛顿环

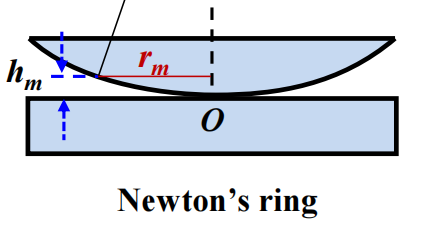
牛顿环

增透膜与高反膜

汽油膜，肥皂泡，昆虫翅膀

厚度均匀的薄膜发生的干涉，入射光为平行光，各个方向的干涉增强被分离出去

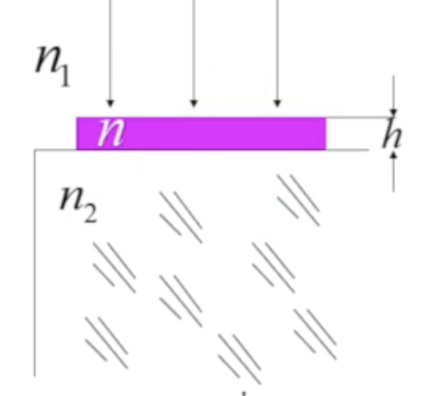
增透膜

n2的反射光被干涉相消，根据能量守恒，透射光会更多

折射率
$$
n=\sqrt{n_1n_2}
$$
$$
n_1 < n < n_2
$$

厚度
$$
h=\frac{\lambda_0}{4n}
$$

增透膜

增反膜

反射被干涉增强，透射光会减少

折射率
$$
n > n_1 且 n > n_2
$$
厚度
$$
h=\frac{\lambda_0}{4n}
$$

等倾斜角干涉

等倾干涉

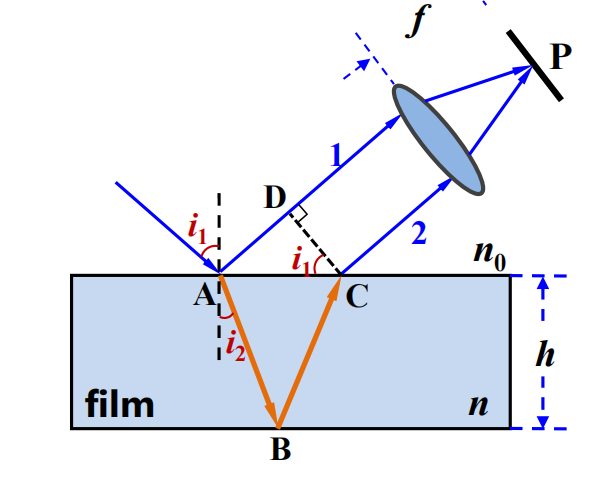
等倾干涉发生在无穷远处

上下表面平行的薄膜发生的干涉，入射光为点光源
$$
\delta = 2nh\cos i_2
$$

半波损失

波从光疏射向光密，在反射过程中会产生$\pi$个相位跃变，我们称之为半波损失

由于半波损失的存在，薄膜干涉明暗条纹的产生条件实际上与杨氏双缝相反
$$
\delta = 2nh\cos i_2 + \lambda/2
$$

等倾图样

内高外低，内疏外密

等倾图样

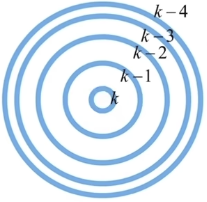
干涉仪

多光束干涉

多光束干涉 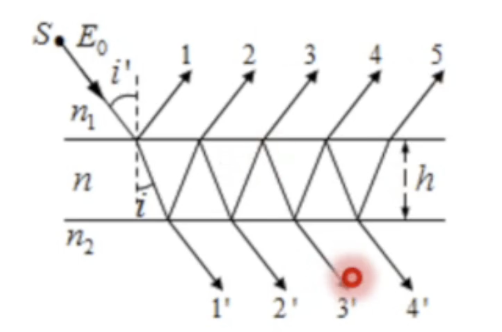$$ \Delta L=2nh\cos i $$ 光在介质内不断反射折射，新的反射折射光强度成等比数列

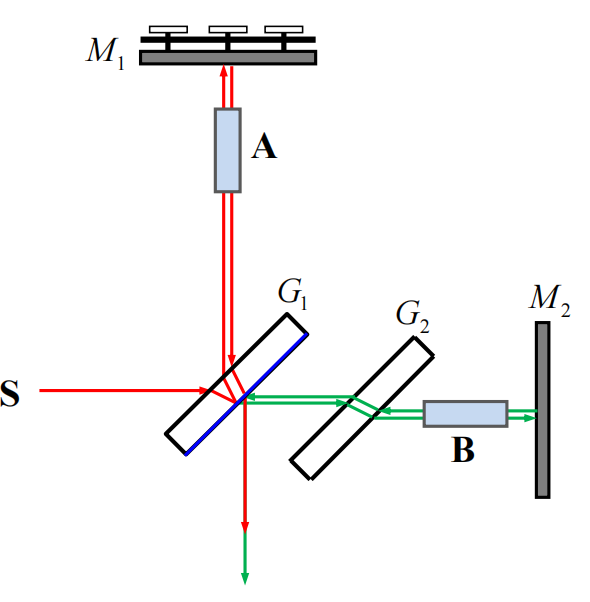
迈克耳孙干涉仪

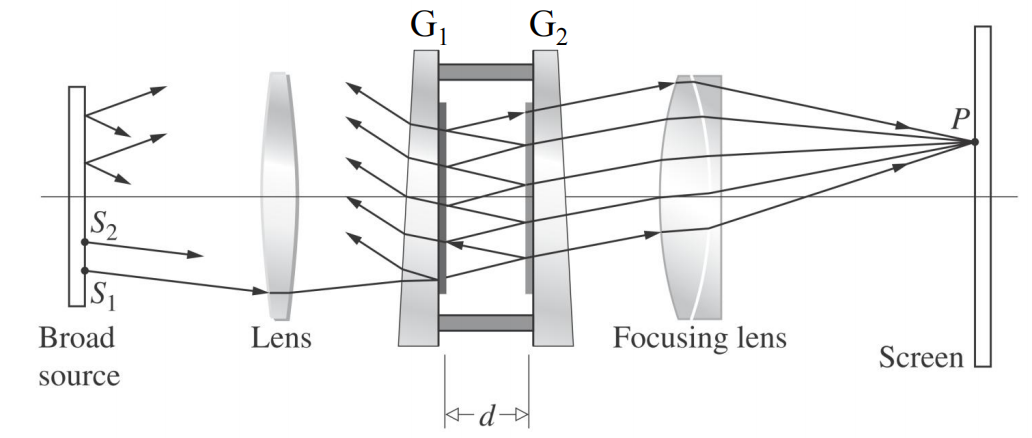
使用分振幅法将两个相互垂直的平面镜等效为空气薄膜，空气薄膜可以等倾，也可以等厚

迈克耳孙

法布里-珀罗干涉仪

由两个梯形透镜组成，用于生成等倾干涉条纹

法布里-珀罗

更新于：2024年7月1日

光学

评论