十:各向异性
内容概述
- 光在各向异性的介质中的传播
- 偏振
双折射晶体
透过双折射晶体(比如方解石晶体),在某些角度只有一个像,在某些角度会有两个像
双折射
现象:一束光经过晶体后被分为了两束光
我们称之为o光和e光
- o光:按折射定律传播的光
- e光:不按折射定律传播的光
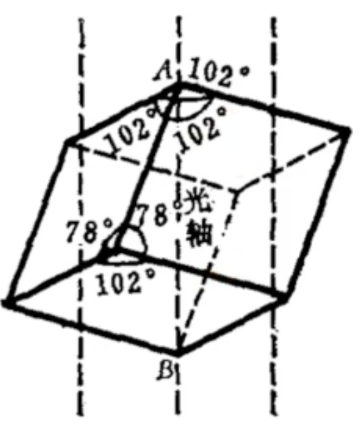
光轴:光束沿着光轴传播时,o光和e光不分开(这个方向两个折射率是相同的)
-
主截面:界面法线和光轴构成的平面
-
主平面:晶体内光线和光轴构成的平面
o光和e光都是线偏振光,o光的振动方向与主平面垂直,e光的振动方向与主平面平行
- 单轴晶体:只有一个光轴的晶体,比如方解石、石英
- 双轴晶体:有两个光轴方向的晶体,比如云母、蓝宝石、硫磺
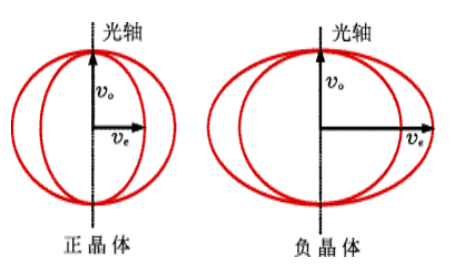
o光和e光的光速不同,波面形状也不同
- o光沿各个方向的传播速度相同,于是波面是一个球
- e光沿着不同方向传播速度不同,我们特别的选取垂直于光轴的面作为e光的波面,这个波面是一个椭圆
- 这两个椭圆是相切的,但大小不确定
- 若o光比e光大,那么是正晶体
- 若o光比e光小,那么是负晶体
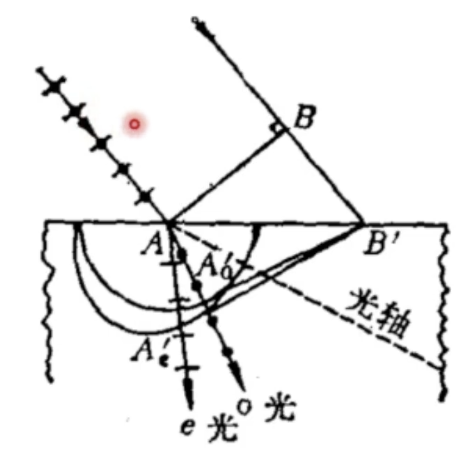
惠更斯作图法
- 偏振态:我们在光线上各距离绘制短线和圆点,用来表示偏振
- 短线表示偏振沿着纸面
- 点表示偏振垂直纸面
- 自然光横线和点的数量应该一样多
绘制折射光
- 过A点做边缘光线的垂线AB,垂足为B
- 我们能求出光线的传播时间$t=\overline{BB’}/c $
- 以A为圆心,做一个半径为$\mathrm{v}_o t$的圆,这是o光波面
- 以A为中心,做一个半轴为$\mathrm{v}_o t 和 \mathrm{v}_e t$的椭圆,椭圆要和圆在光轴处相切
- 从B’出发做圆和椭圆的切线,切点为$A’_o,A’_e$
- o光折射光为$AA’_o$
- e光折射光为$AA’_e$
光的偏振
由于晶体可以分离o光和e光,因此可以做成偏振器
光的偏振状态
回忆一下
光有五种偏振状态
- 自然光
- 部分偏振光
- 线偏振光
- 圆偏振光
- 椭圆偏振光
光偏振状态的检验:将光通过检偏器,旋转检偏器,通过光强的变化判断
- 无变化:自然光、圆偏振光
- 有变化但没有消光:部分偏振光、椭圆偏振光
- 有变化且有消光,线偏振光
仅通过检偏,只能简单分出三类光,无法更近一步区分偏振态,而使用晶体可以明确知道偏振态
马吕斯定律:线偏振光经过检偏器,光强满足
$$
I=I_0\cos^2\varphi
$$
布鲁斯特定律:光线以大于布鲁斯特角入射,反射光是线偏振光
$$
\tan i_B=\frac{n_2}{n_1}
$$
光在晶体中的传播
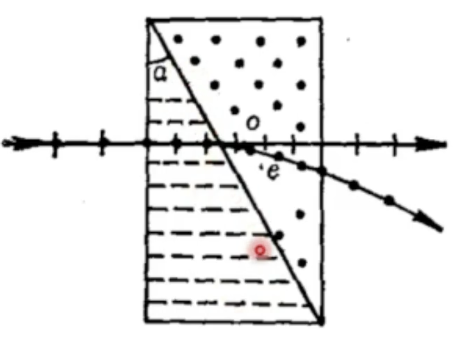
洛匈棱镜
由两块冰洲石构成
- 左侧光轴平行纸平面和入射光,光线进入时不会发生双折射
- 右侧光轴垂直纸平面,光线进入后o光变e光,e光变o光
沃拉斯顿棱镜
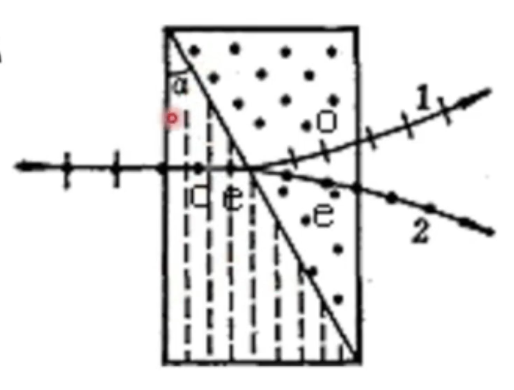
- 光线进入左侧,o光和e光方向不变,速度改变,e光会比o光快
尼科尔棱镜
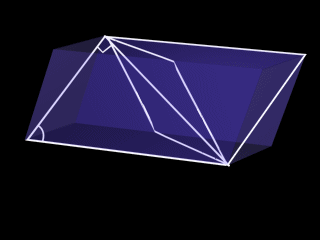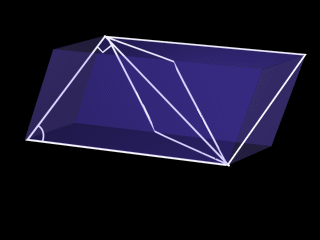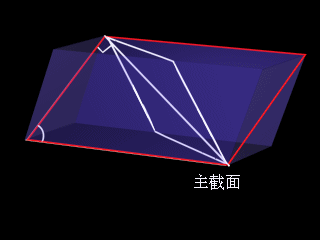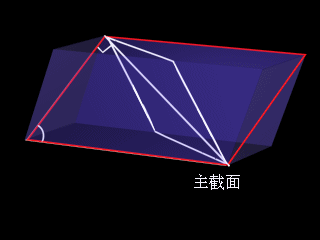
偏振光的获取和检验
核心思想为垂直振动和合成,任何一个偏振态,都是两个垂直振动的合成
所有偏振态都是由两垂直的线偏振光合成,两者的相位差$\delta$将决定合成的是何种偏振光
$\lambda/4$波晶片能带来$\pi/2$的相位差
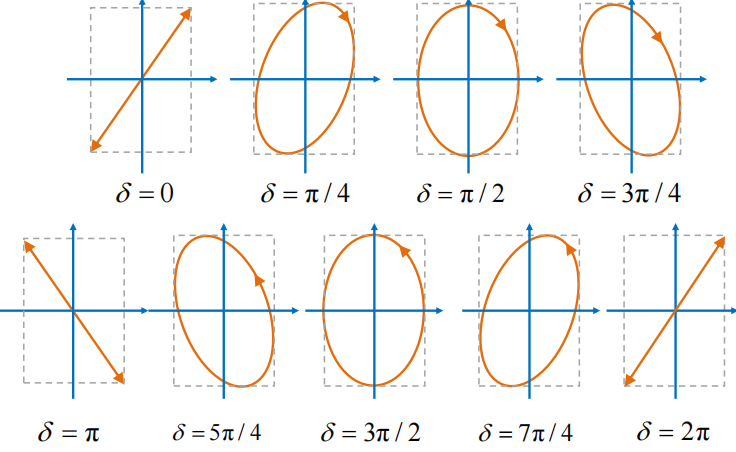
光通过晶体时,o光和e光可能方向不变,相位差改变,通过调整两者间相位差,就能得到圆偏振、椭圆偏振
求出射光偏振态
出射光相位差=入射光相位差+波晶片相位差

偏振光检验
- 使用偏振片将五种偏振光变为三组
- 对于自然光和圆偏振光那一组
- 光线继续通过$\lambda/4$波晶片,如果变为线偏振光,则为圆偏振光
- 对于部分偏振光和椭圆偏振光那一组
- 将偏振片旋转至光强最强处
- 将$\lambda/4$波晶片光轴旋转至与偏振片透振方向平行
- 去除偏振片,光线继续通过$\lambda/4$波晶片
- 此时o光和e光与椭圆主轴一致,若变为线偏振光,则为椭圆偏振光

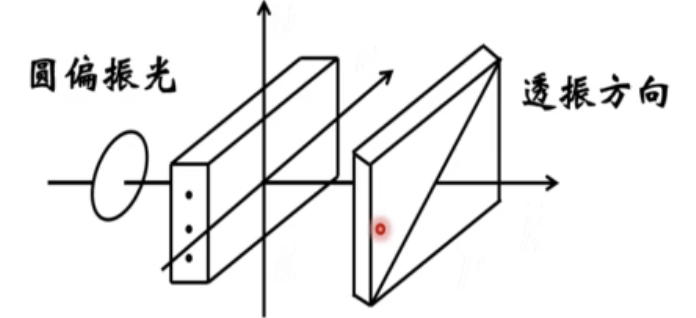
左右旋检验
一个圆偏振片,通过$\lambda/4$波晶片,再通过透振方向为斜对角线的偏振片
- 旋转偏振片,若发现有消光位置,则停止旋转(圆偏振通过波晶片变线偏振,透过偏振片会有消光),此时透振方向和线偏振光偏振方向垂直
- 若透振方向为一三象限,入射光为右旋
- 若透振方向为二四象限,入射光为左旋