五:反射与折射
内容概述
- 光在单层各项同性表面的反射与折射
- 菲涅尔方程
- 全内反射
- 相位突变,布鲁斯特角
菲涅尔方程
菲涅尔方程
各项同性介质(Isotropic medium):折射率处处相同的材质
光密介质:折射率高的介质(这是一个相对概念)
光疏介质:折射率低的介质(这是一个相对概念)
在几何光学中的那些反射方程,只能得到入射光、反射光、折射光间的方向关系
而菲涅尔方程(Fresnel Equations)可以求出反射光、折射光的振幅、相位、偏振
菲涅尔方程的边界条件表明:磁场和电场在边界处连续,也就是入射光的电场磁场=反射光+折射光的电场磁场
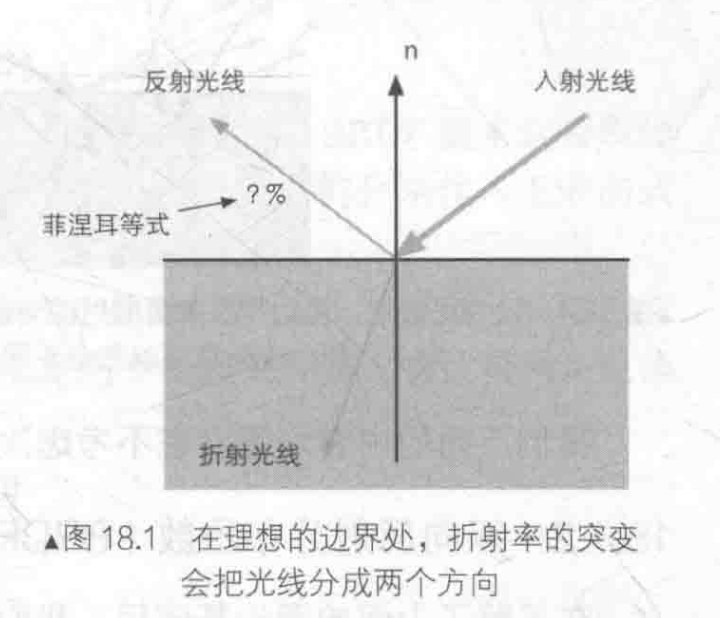
我们将入射光的电场分为两个部分,方向满足右手正交系
- 平行(parallel)于平面的电场$E_p$
- 垂直(senkrecht)与平面向外的电场$E_s$
经过复杂的推导,我们能得到
$$
r_p=\frac{E_{1p}’}{E_{1p}}=\frac{\tan(\mathrm{i_1}-\mathrm{i_2})}{\tan(\mathrm{i_1}+\mathrm{i_2})} \\
r_s=\frac{E_{1s}’}{E_{1s}}=-\frac{\sin(\mathrm{i_1}-\mathrm{i_2})}{\sin(\mathrm{i_1}+\mathrm{i_2})} \\
t_p=\frac{E_{2p}}{E_{1p}}=\frac{2\cos \mathrm{i_1}\sin \mathrm{i_2}}{\sin(\mathrm{i_1}+\mathrm{i_2}) \cos (\mathrm{i_1}-\mathrm{i_2})} \\
t_s=\frac{E_{2s}}{E_{1s}}=\frac{2\cos \mathrm{i_1}\sin \mathrm{i_2}}{\sin(\mathrm{i_1}+\mathrm{i_2})}
$$
- $r$:反射光
- $t$:折射光(透射光,Transmission)
于是我们能得出几个结论
- 反射光、折射光与入射角、折射率有关
- $p$与$s$是独立的
菲涅尔方程的含义
外反射
外反射(External reflection):从折射率低射向折射率高,比如从空气射向玻璃

我们发现,随着入射角的增加
-
折射一直是正数,并且两个方向没有明显差异
-
$r_s$一直是负数,而$r_p$先正后负
-
布鲁斯特角(Brewster’s angle,图中$i_B$),在此处$r_p$发生了一个$180^{\circ}$的相变
-
当入射角为$90^{\circ}$时,也就是掠射角(grazing angles),我们发现此时完全不发生折射,只发生反射
- 对于一个湿表面,远看发现很亮,近看却发现变暗了
- 远看水面,大部分光来自反射,于是波光粼粼;近看水面,折射部分加强,于是清澈见底
-
让入射角为$0^{\circ}$,也就是垂直入射时,$r_p$完全反向反射回来,折射很微弱
内反射
内反射(Internal reflection):从折射率高射向折射率低,比如从玻璃射向空气
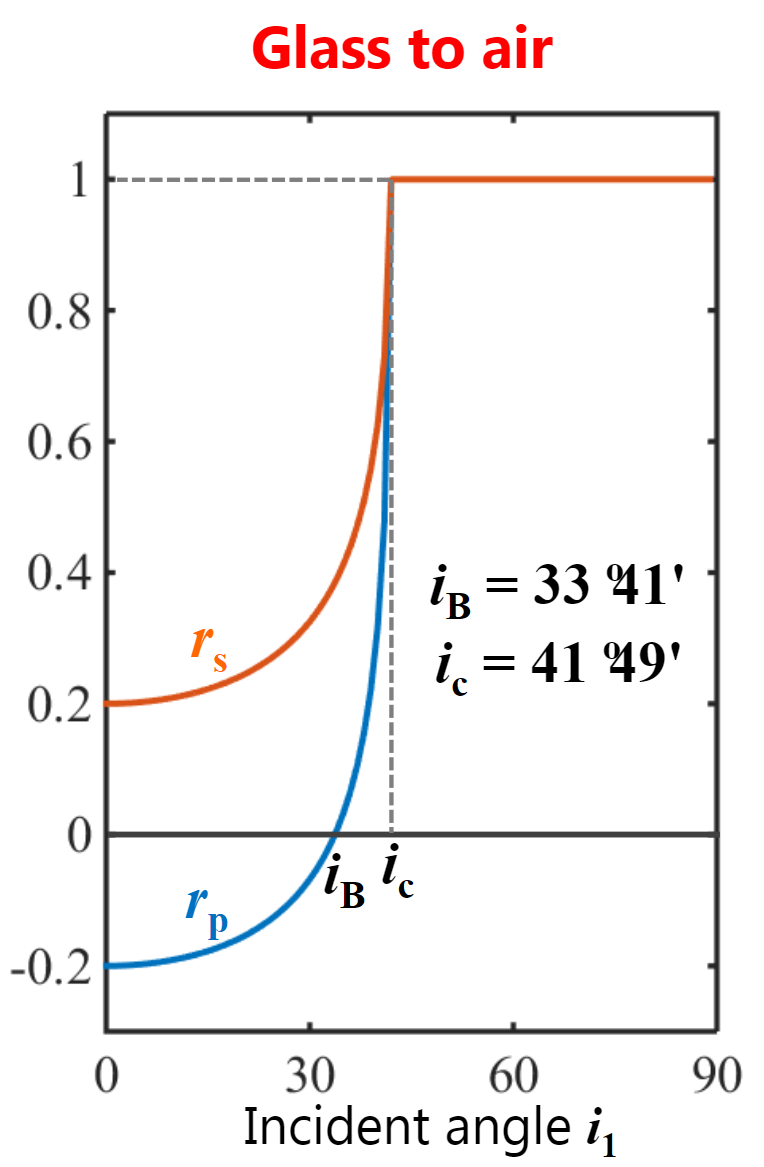
- $t_p=t_s$,两者没有相位差
- 当$i=i_c$,此时$r_p=r_s=1$,我们称之为全内反射(Total Internal Reflection,TIR),$i_c$被称为临界角(critical angle)
相位移
相位移(Phase shift)
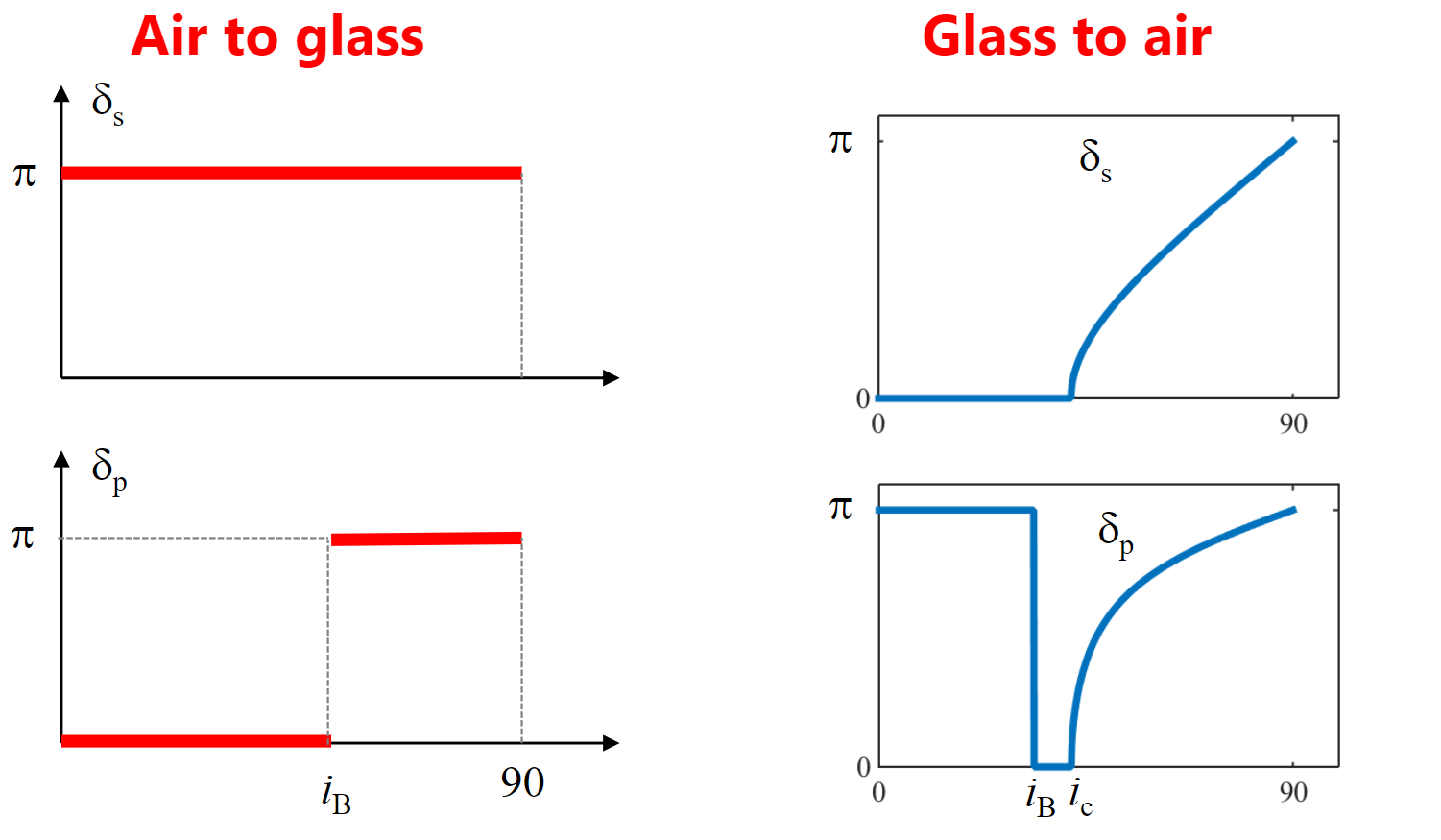
-
从低折射率到高折射率,会有一次$\pi$相位移
-
从高折射率到低折射率,没有相位移
薄膜相位移:光线在薄膜内发生多次反射,可能会附加一段相位移
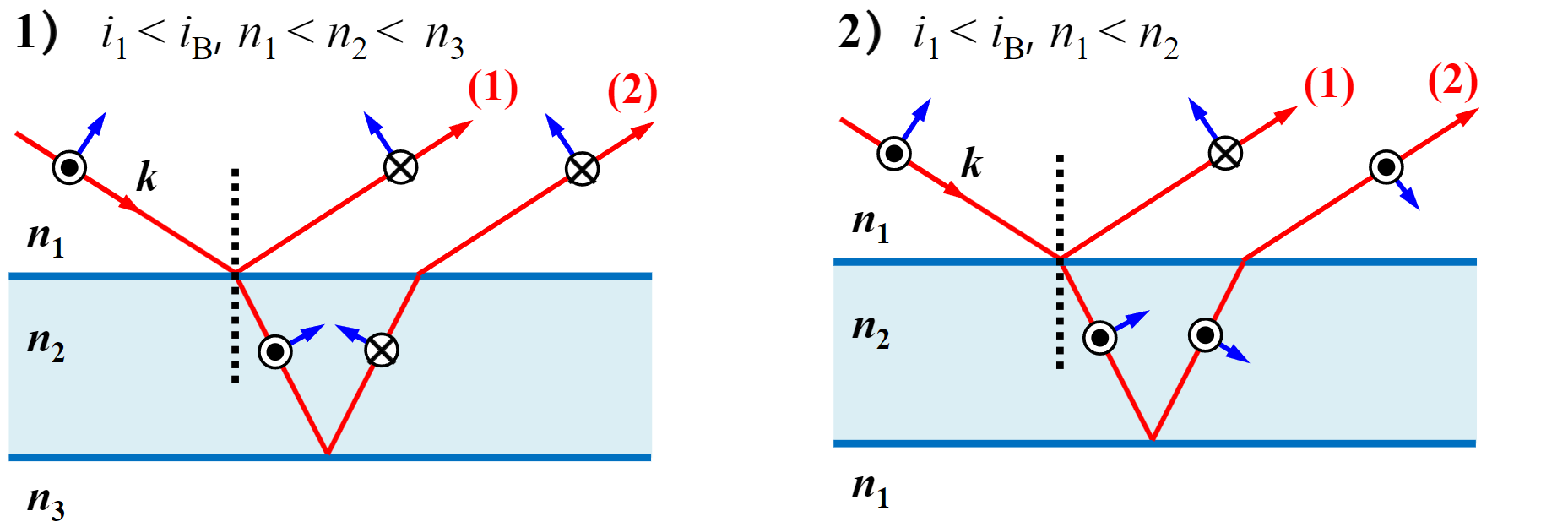
简化菲涅尔方程
反射比(Reflectance,用$R$表示):反射光占入射光的能量
折射比(Transmittance,用$T$表示):透射光(折射光)占入射光的能量
能流(Energy flow):单位时间内通过单位横截面积的能量
能流 = 辐照度 x 横截面积
$$
R=r^2
$$
$$
T=\frac{n_2\cos i_2}{n_1\cos i_1}t^2
$$
根据能量守恒定律(Energy conservation law):$R+T=1$
当垂直入射时,带入菲涅尔方程,得到
$$
\begin{cases}
r_p=\frac{n_2-n_1}{n_2+n_1} \\
r_s=-r_p \\
t_p=\frac{2n_1}{n_1+n_2} \\
t_s=t_p
\end{cases}
$$
于是得到
$$
R_p=R_s=\left( \frac{n_2-n_1}{n_2+n_1}\right)^2
$$
$$
T_p=T_s=\frac{4n_1n_2}{(n_1+n_2)^2}
$$
对于空气($n_1=1$)和玻璃($n_2=1.5$),$R=0.04,T=0.96$
这也是为什么图形学中取 0.04为F0的基准值
为什么晚上室内玻璃像镜子一样?
- 晚上的玻璃,$R\approx 0.08$,室内的光线大部分都会反射回来,而室外的光线只有很少才会透射进来,看到的光绝大多数都来自室内的反射光,因此像镜子一样
- 此外,夜晚室内光线本身也比室外光线强
为什么白天从黑暗的房间看外面看,看的很清楚,而从室外向里看,却看不清?
单透玻璃的原理是什么?
金属
金属(电介质)表面存在大量自由电荷,在外部电场的作用下,自由电子在固体表面(相对固定的金属阳离子)间不断弹跳
德鲁德模型
德鲁德模型(Drude model)是一种描述金属表面自由电子运动的模型(很复杂,看一下,图一乐)
$$
P=-nex
$$
$$
m\frac{\partial^2 x}{\partial t^2}+m \gamma \frac{\partial x}{\partial t}=eEe^{-\mathrm{i}\omega t}
$$
- 偏振度(用$P$表示,在电磁波那一章在介绍洛伦兹震荡时有一个极其类似的公式)
- 阻尼率(damping rate,用$\gamma$表示)
- 电荷密度(density of electron,用$n$表示)
这个推导很复杂,又涉及复变函数之类的,直接给结论:当平面波垂直射向金属时,$R \approx 1$
布鲁斯特角
布鲁斯特角(Brewster’s angle),在外反射那一节提到过,当$i_1=i_B,r_p=0$
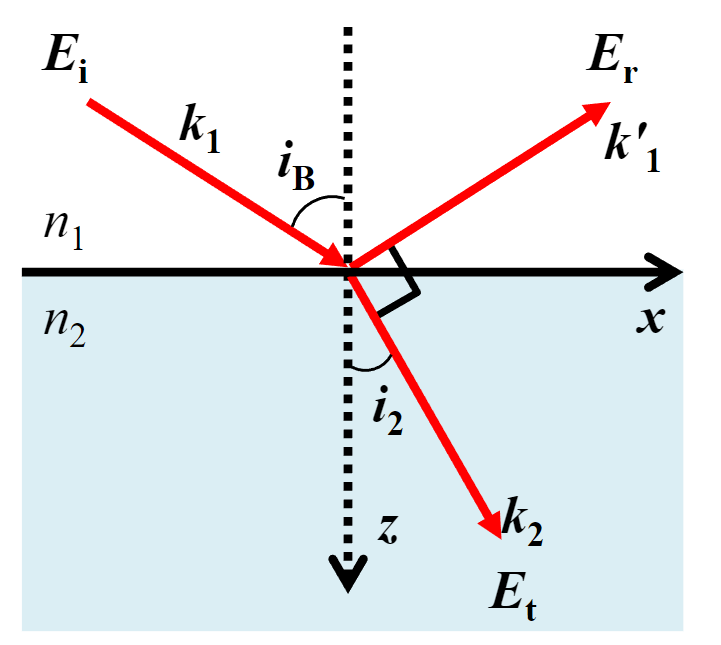
一个应用是测量不透明介质的折射率
$$
\tan i_B=\frac{n_2}{n_1}
$$
另一个一个应用是制作偏振器,激光经过偏振器后,射出的光线是线偏振的
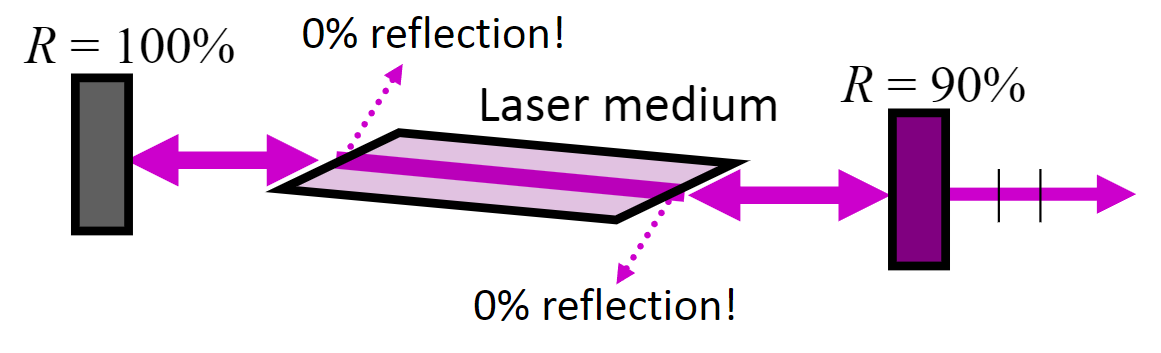
自然光(非偏振光)的反射光、折射光是偏振光,但如果给镜头安装偏振器,并适当旋转偏振片,使偏振片的透振方向与反射光的透振方向垂直,此时$i_1=i_B,r_p=0$,不发生反射,只发生透射,于是会看得更清晰

偏振
线偏振光的反射、折射光仍为线偏振光,但其光矢量方向会发生改变(上为入射光,下为反射光)
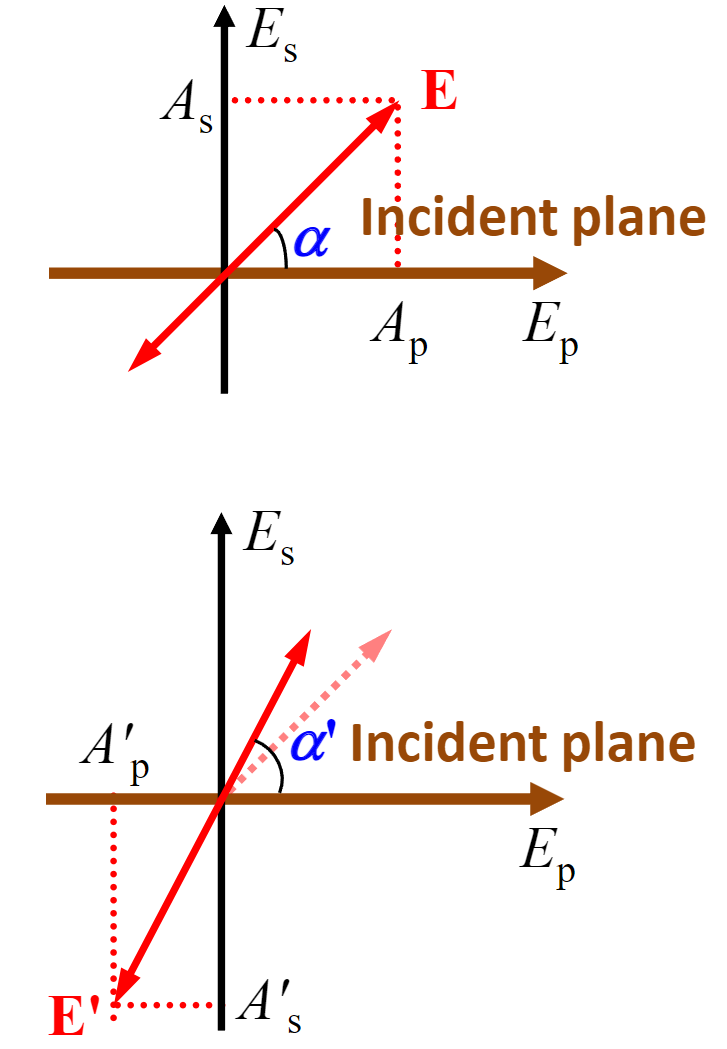
圆偏振/椭圆偏振光的反射折射光一般为椭圆偏振光
全内反射
从折射率高射向折射率低,当入射角满足$i_1 \ge i_c$时,就会发生全内反射(Total internal reflection)
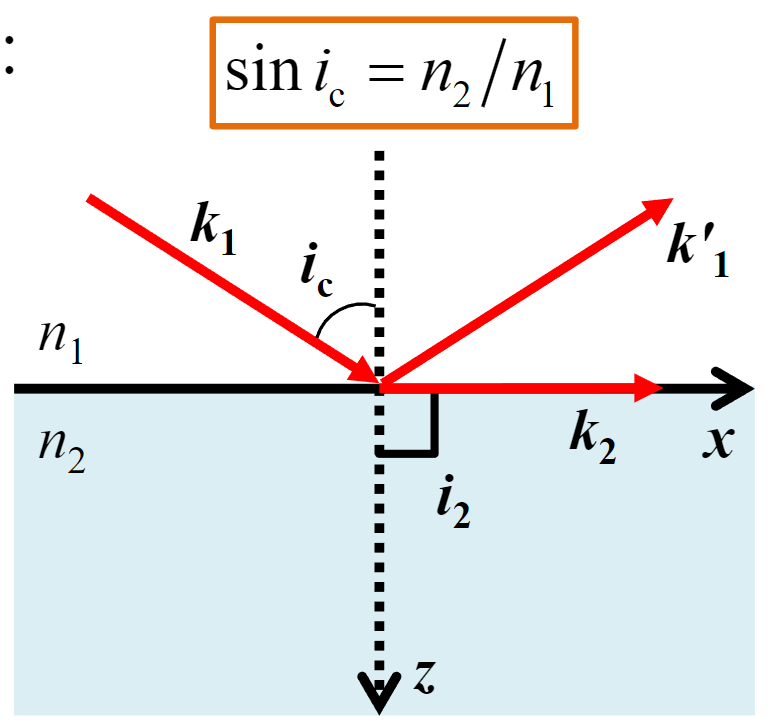
此时$R\equiv 1$,也就是所有能量都被反射,不发生透射,于是低折射率那一侧看不到任何光,物体变黑了,这个现象就是全内反射
全内反射的应用:棱镜(Prisms)、光纤
隐失波
隐失波(Evanescent wave) :光从光密介质入射光疏介质时,如果发生全内反射,光疏介质那一侧产生的电磁波
隐失波的振幅随着穿透深度(Depth of penetration)的增加而呈现指数衰减,随切线方向而改变相位,因此是一种表面波
$$
d=\frac{\lambda_2}{2\pi \Omega}
$$
- 穿透深度:与分界面的垂直深度,用$d$表示
- $\sqrt{1-\sin ^2 i_2} \equiv \mathrm{i}\Omega$
隐失波沿着z轴衰减,沿着x轴传播
$$
E_2=E_{02}e^{-z/d}e^{\mathrm{i}(k_xx-\omega t)}
$$
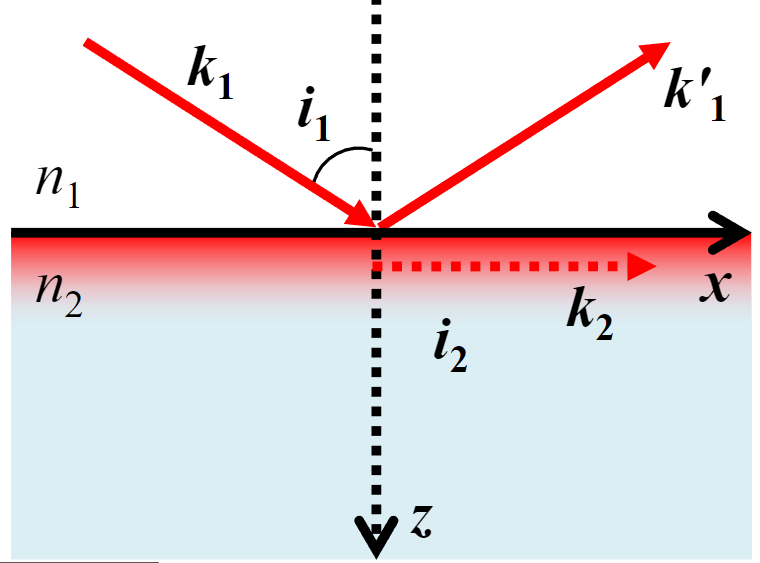
隐失波不是横波
隐失波的一个应用是制作分光镜,如果只有一个棱镜(下图黑色三角形),会发生全内反射,光线全部反射
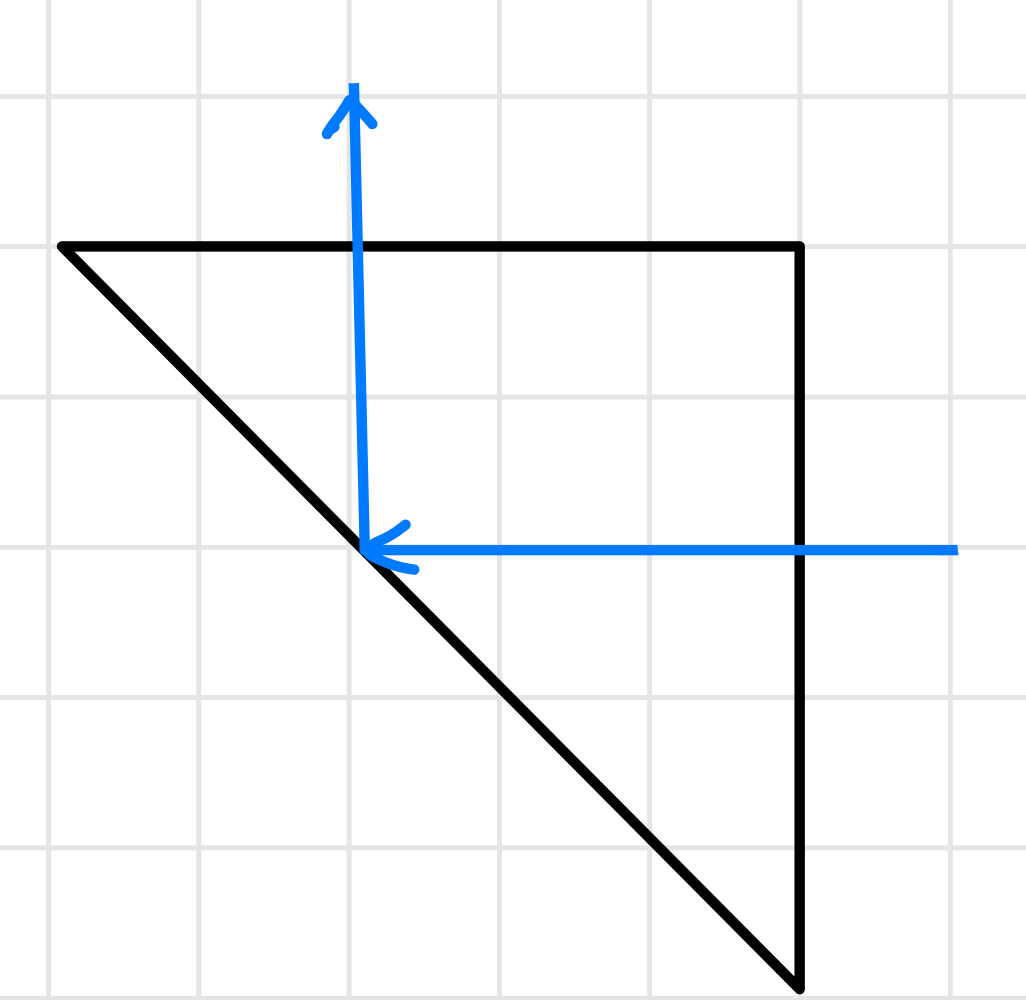
如果将两个棱镜靠近,通过控制两者间空气的间隙,在隐失波的作用下,能实现分光
其他应用:
- 光子隧穿
- 近场扫描显微镜
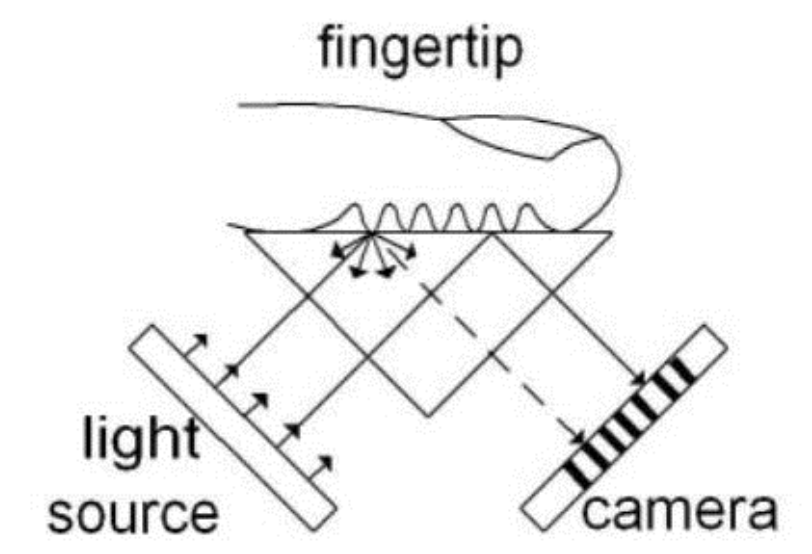
- 指纹检测