抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

Reuben Sun

主页

图形

引擎

AI

编程

数学

光学

DCC

游戏

光学：几何光学

optics

发布于：2023年1月31日

四：几何光学

几何光学，也被称为射线光学（Ray optics），忽略光的波动性，以几何方法来研究光在均匀介质中的传播

基本定律

几何光学包含两个部分，一个是光学三定律，定性描述了几何光学中光的传递，一个是费马原理，定量计算了光的传播（通常为光学元件间近轴传播）

光学三定律

  • 光在均匀介质中沿直线传播
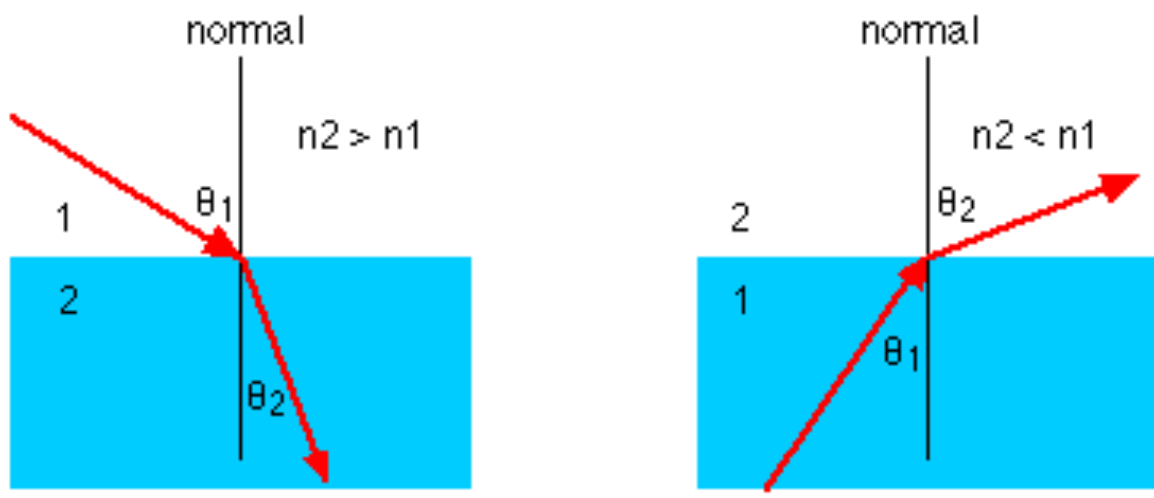
  • 光的反射、折射定律
    • 反射角等于入射角
    • 入射角与折射角的正弦值之比等于折射率之比（Snell定律）
  • 光独立传播，光路可逆

Shell定律
$$
n_i\sin \theta_i= n_t \sin \theta_t
$$

Snell

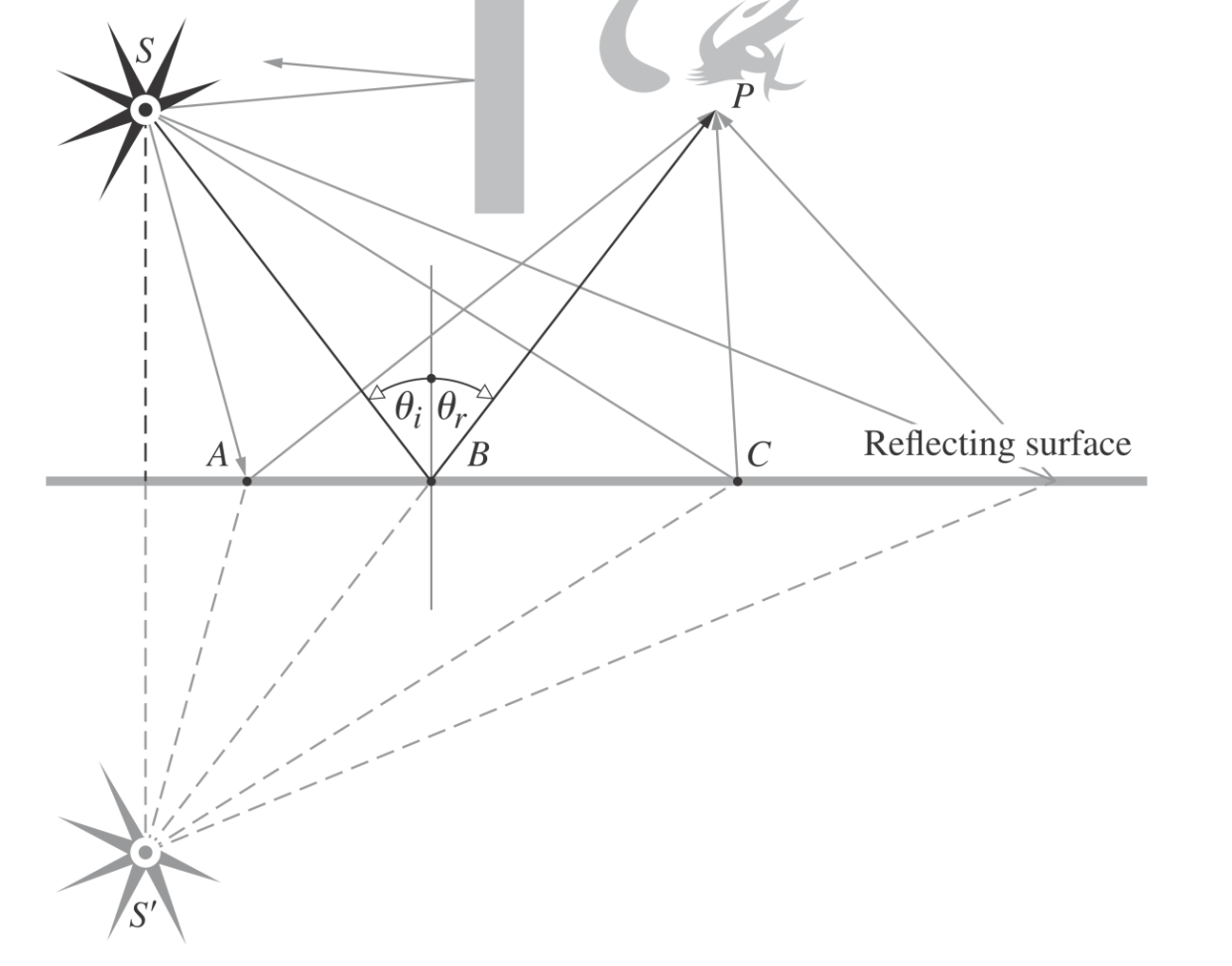
反射光线是最短路径（亚历山大）

亚历山大

光程

由于光在介质中移动速度不同，为了方便描述光在介质中移动某段距离要花费的时间，我们引入了光程长度。于是我们在计算时就可以认为光速永远不变，只是光的传播距离与现实距离不同

光程长度（Optical path length，OPL）：光在介质中传播长度与介质的折射率的乘积
$$
[l]=ns
$$
光程描述的是：光在该介质中移动真实距离所花费的时间，如果在真空中能运动多远的距离

费马原理

开创了以“路径积分，变分原理“来描述物理规律的思维方式

费马原理（也叫最短时间原则）：

  • 光在两点间的传播路径是最短路径（最短路径可以由多条，但是其光程相同）
  • 两点间的光程恒定（光程函数的导数为0）

费马原理可以推导出光学三定律

在均匀介质中折射率为常数，光在两点间的传播路径为最短距离，又由于两点间直线距离最短，因此光沿着直线传播

由于反射点、折射点都在交线OO‘上，因此他们在同一平面内（在交线上距离最短）

由于两点间直线最短，沿着反射轴做反射光线的对称直线，发现当反射角等于入射角时，入射光线和对称光线为一条直线

用折射率和三角形长度表示折射光线的光程，该光程应该是最小值，因而导数为0，求导化简得出Shell公式

透镜成像

根据费马原理，两点间光沿着光程最短的路径传播，这说明凸透镜成像中每一条光线的光程都相等

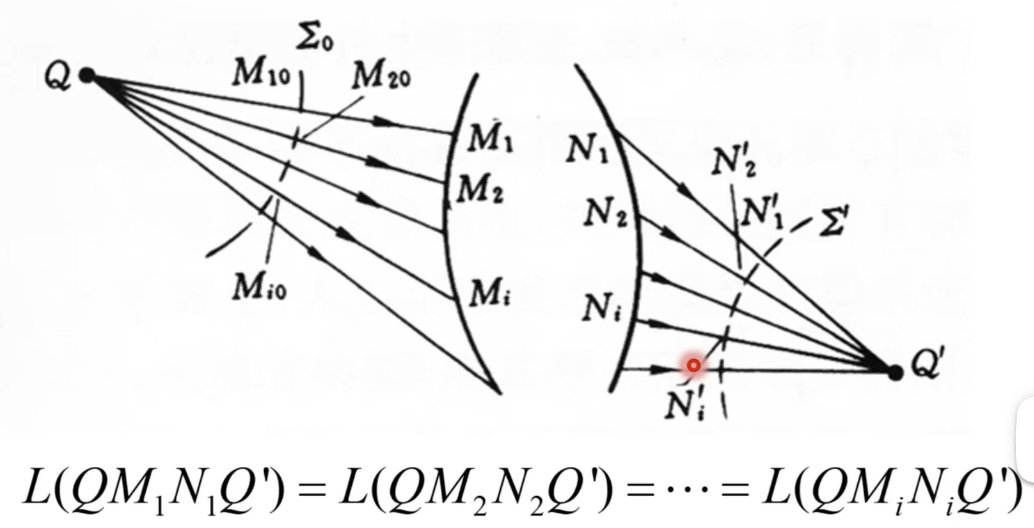
费马原理透镜

实际上，凹透镜散射光光线的反向延长线与入射光组成的总光程也是根根相等的

等光程

等光程：如果一个光学器械每条光线都是等光程的（比如透镜），我们称之为等光程，他们可以严格成像

不等光程的器械不能成像，近似光程的器械能成模糊的像

费马原理的应用

反曲椭球面生成平行光：从椭球面焦点发生灯光，会生成平行光，由于平型光不会汇聚，因此他们的光程为无穷大

光在椭球面内反射：在椭球面内，两个焦点间光程为恒定值（毕竟椭圆上的点到两个焦点距离的和为焦距）

双曲透镜将平行光汇聚到一点

半球面反射

半球面

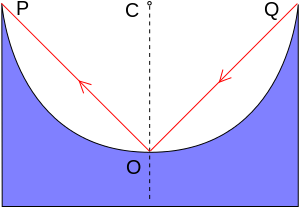
成像

光学系统（Optical system）：一个包含一个或多个光学元器件的系统

物体空间（Object space）：入射光线所在的区域

图像空间（…/…/images space）：出射光线所在的区域

理想光学系统（ideal optical system）：物体能被完美地成像，比如平面镜反射

共轭点（conjugate points）：物体点和图像点组成共轭点

对于一个理想光线系统，每对共轭点的光程（后面以OPL指代）均相同

实像：物体发出的光经过反射、折射后，汇聚成新的像，被称为实像（比如凸透镜）

虚像：物体发出的光经过反射、折射后，变成了发散光线，将其反向延长得到的像，被称为虚像（比如凹透镜、平面镜）

单心性

从一点发射光源，经过光学系统后，仍然汇聚为一点，那么这个光学系统满足单心性

平面镜反射满足单心性，折射不满足

不满足单心性，物像和图像不共轭，不能完美成像

全反射

当光从光密射入光疏，且角度大于某个值后，只发生反射，不发生折射

光导纤维

不过光疏介质介质中并没有没有透射波，但这些透射波与界面平行，且振幅在垂直界面方向按指数衰减，于是很快就没了，这个波被称为隐失波

人眼为什么能看到虚像

人为什么能看到东西？是因为物体经过眼睛，在视网膜上成了像，在这里，眼睛是成像系统

我们在讨论实像虚像时，提到的光学系统那些透镜们，于是虚像的全称应该是“某物体在xxx光学系统的虚像”，人眼并不是看到了“某物体在xxx光学系统的虚像”，而是在该处，经由人眼，看到了一个实像

理想光学系统

  • 共轭性：物像种每个点、线、面都能在图像上找到对应的点、线、面
  • 等光程

棱镜成像

偏向角

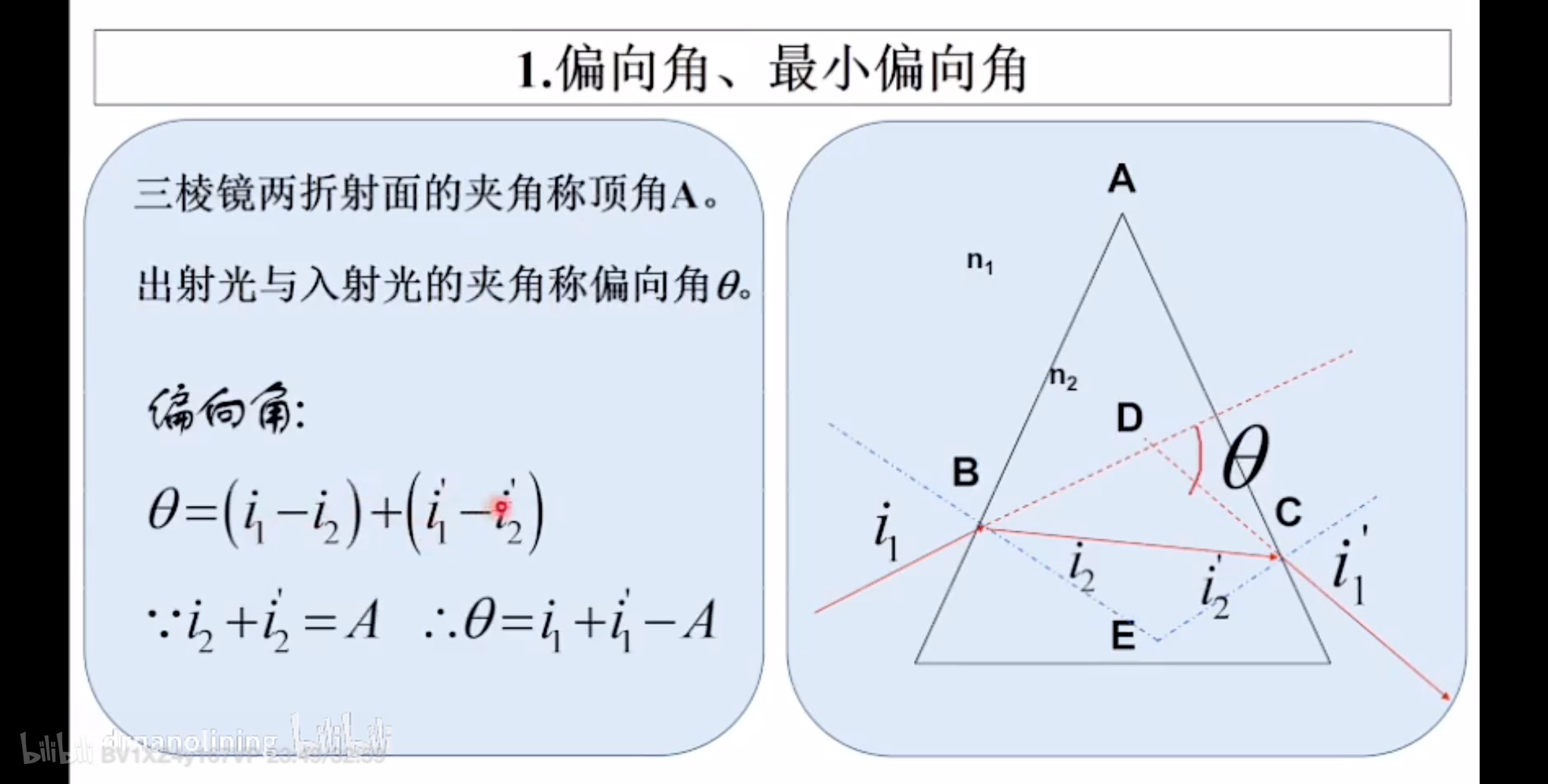
球面成像

尽管球面不是一个很好的光学器械，但比较好加工（其实现在加工技术已经很好了，很多人的眼镜都是非球面的），于是球面成像是几何光学很重要的一块

光轴：若一个光学系统由球面组成，各球心的连线在一条直线上，该光学系统被称为共轴球面系统，这条直线被称为光轴

球差

我们上面提到球面不是一个很好的光学器械，因为透镜成像有球差

透镜成像，靠近光轴的光会被汇聚在靠后的位置，远离光轴的光会被汇聚在靠前的位置，也就是透射光经过球面成像后不再汇聚为一点，单心性被破坏

球差

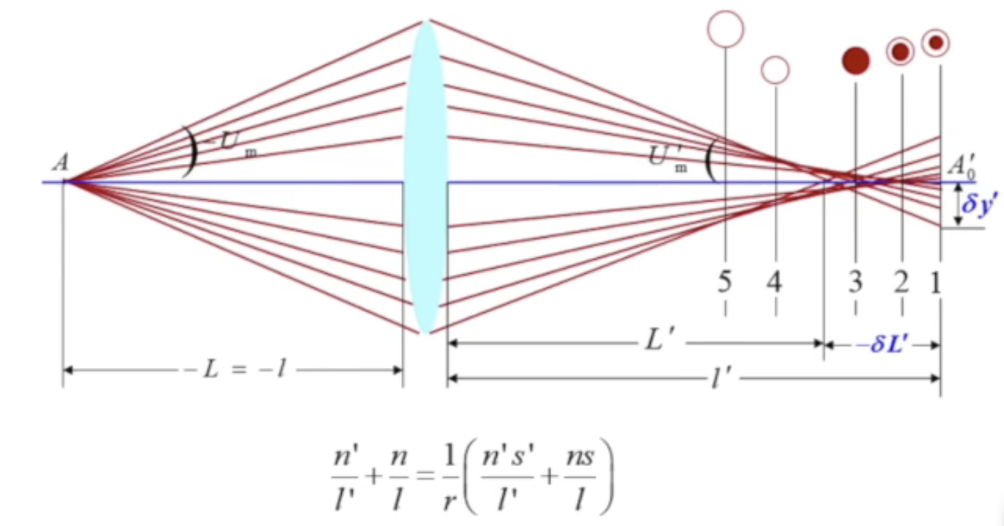
近轴条件

由于球差的存在，我们假设光只在近轴处传播，于是“消除”了球差

近轴条件（paraxial condition）：入射角与光轴（optical axis）的夹角（用$u$表示）小于等于$5^{\circ}$

近轴条件

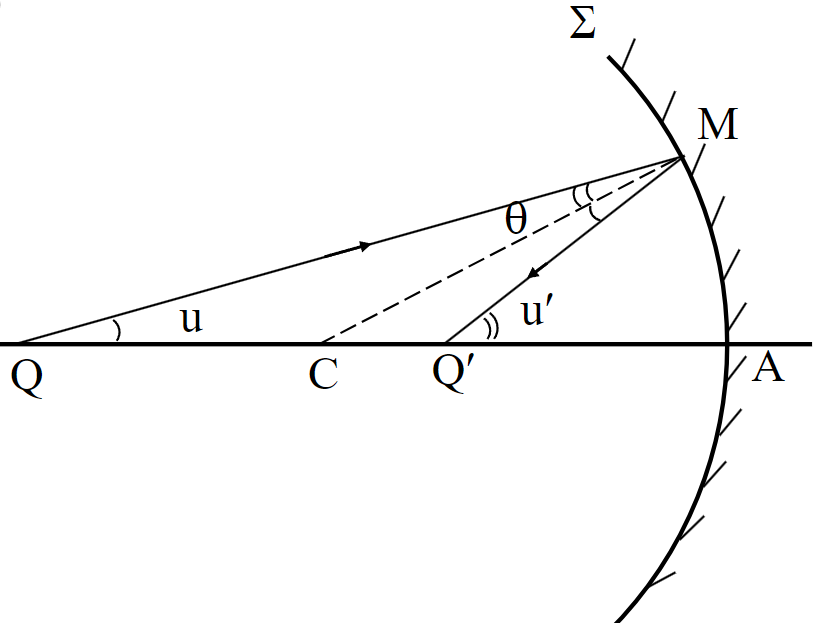
此时，三角函数可以近似
$$
\cos u \approx 1 \
\sin u \approx u \
\tan u \approx \sin u
$$

消球差平面（Aplanatic Surface）：允许所有光线在两点之间以相等的OPL传播的表面

消球差

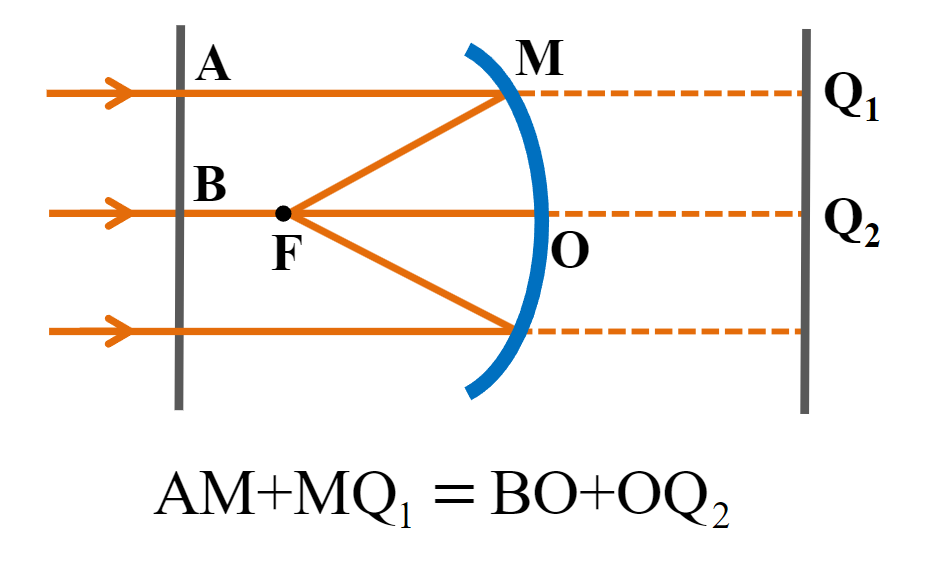
符号法则

简单来说，若左侧的光射向一个左凸的球面在右侧汇聚，距离都是正的

设入射光从左向右

  • 若入射点在顶点（球面和光轴的交点）左侧，那么入射点到顶点的距离为正，反之为负
  • 若汇聚点在顶点右侧，那么汇聚点到顶点的距离为正，反之为负
  • 若球心在顶点左侧，则半径为负，反之为正

绘图标准

  • 基准点：球面顶点(单球面系统)、焦点
  • 基准线：光轴、各折射点的法线
  • 长度量：由指定原点量起顺光线传播方向为正，反之为负。
  • 高度量：垂直向上为正，反之为负。
  • 角度量规定：以锐角衡量，以主光轴顺时针转到光线为正。
  • 规定：图上只标绝对值。

球面反射

Reflection at spherical surfaces

球面反射

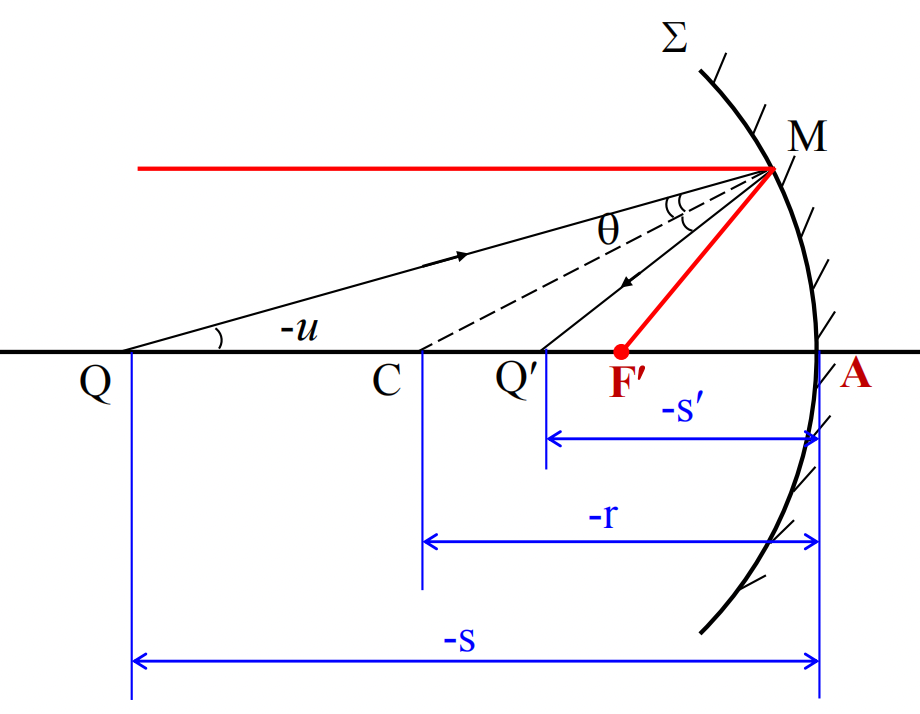
$$
\frac{1}{-s}+\frac{1}{-s’}=-\frac{2}{r}
$$

  • 光轴（QA这条线）
  • 焦点（image focus，图中$\mathrm{F’}$）：平行于光轴的光线打到球面上，会汇集到一点，这个个点被称为焦点
  • 物体焦距（Object focal length，用$f$表示）
  • 图像焦距（…/…/images focal length，用$f’$表示）

在球面反射，物体焦距和图像焦距是相等的
$$
f= \lim_{s’ \rightarrow \infty}s
\
f’= \lim_{s \rightarrow \infty}s’
\
\frac{1}{s}+\frac{1}{s’}=\frac{1}{f}
$$

球面折射

Refraction at spherical surfaces

球面折射
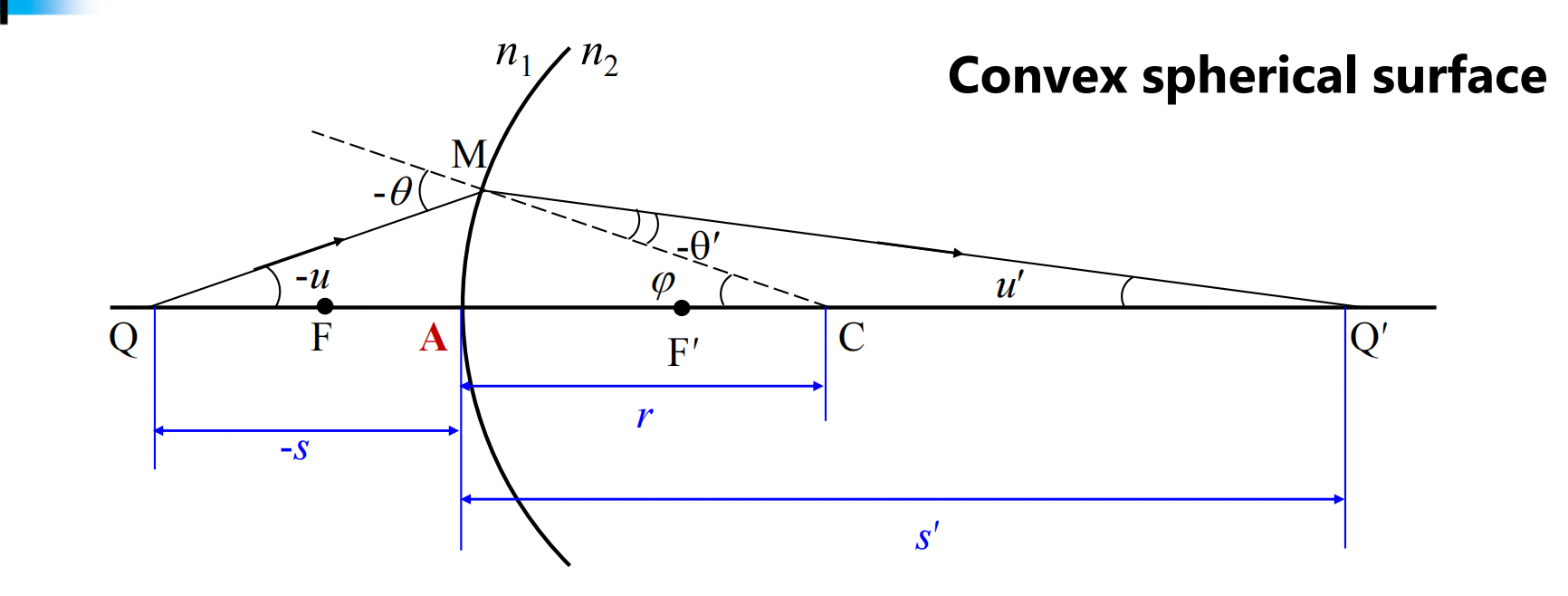
$$
\frac{n_1}{-s}+\frac{n_2}{s’}=\frac{n_2-n_1}{r} \equiv \Phi
$$

  • 光焦度（用$\Phi$表示）：用与描述光线系统对光线的曲折能力

高斯透镜公式（Gaussian Lens Formula）
$$
\frac{f}{s}+\frac{f’}{s’}=1
$$
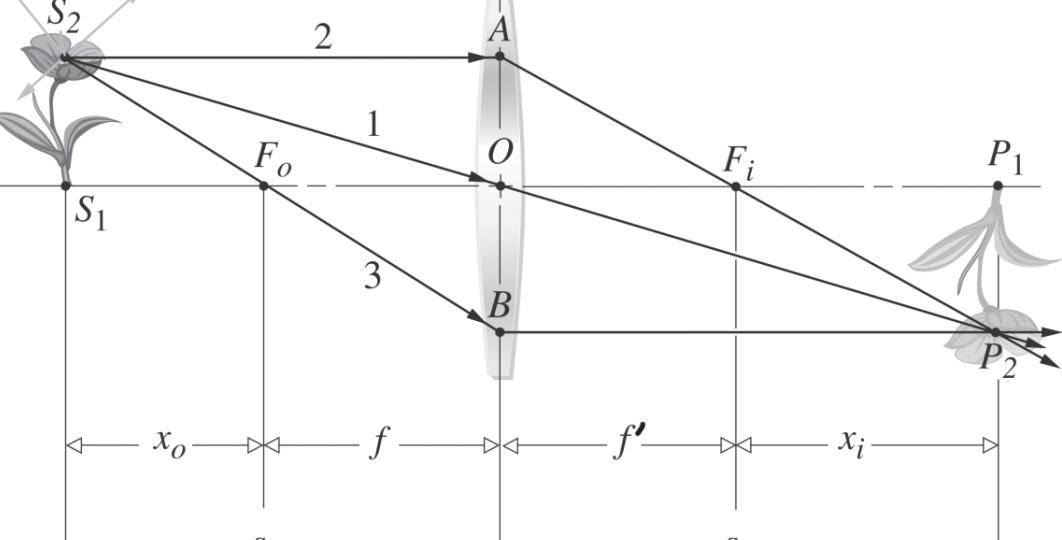
牛顿透镜公式（Newton form of Lens Formula）
$$
x_0x_i=ff’
$$
牛顿成像公式

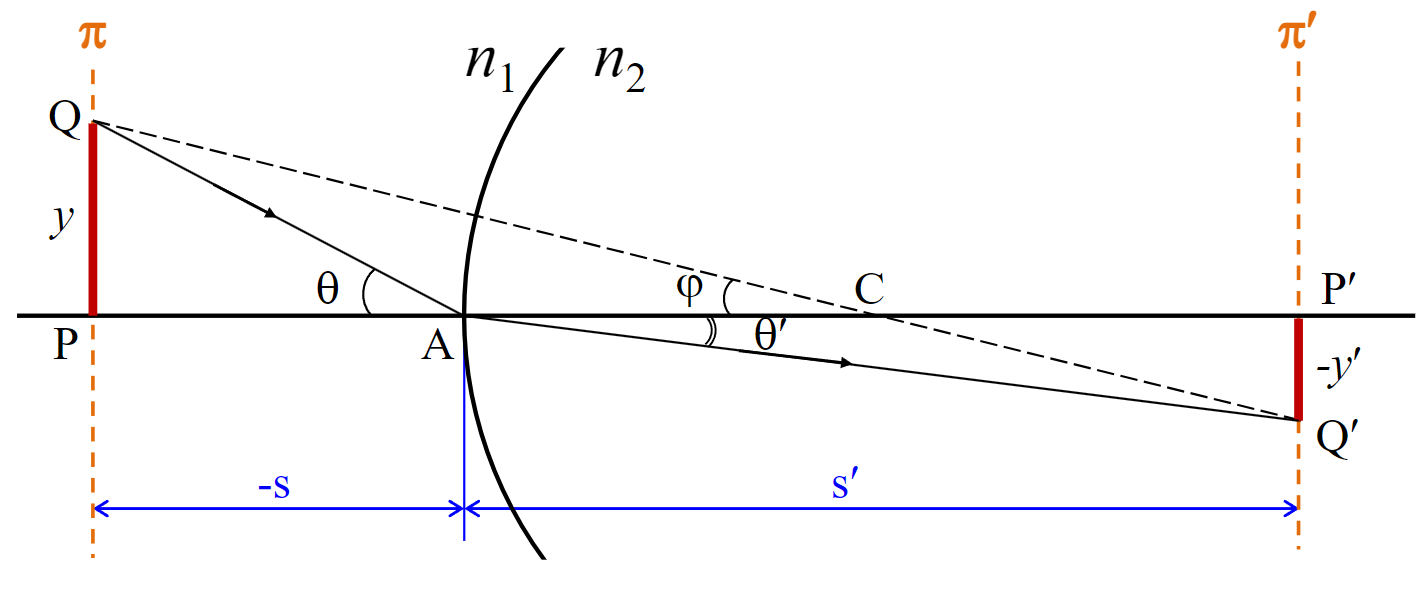
离轴点成像

Imaging for off-axis points

就是y比较大，导致不能使用三角函数近似

离轴成像

薄透镜成像

透镜：由两个同轴折射球组成的镜子，根据球心位置，分为凸透镜（convex lens）和凹透镜（concave lens）

薄透镜（Thin lens）：中心半径和曲率厚度可以忽略不记的透镜

光轴（Optic axis）：连接两个曲面中心的轴

光学中心（Optic center）：两个球面的基准点（vertex）视为重合，重合点就是光学中心

凸透镜分为双凸、平凸、弯凸三种

凹透镜分为双凹、平凹、弯凹三种

透镜公式

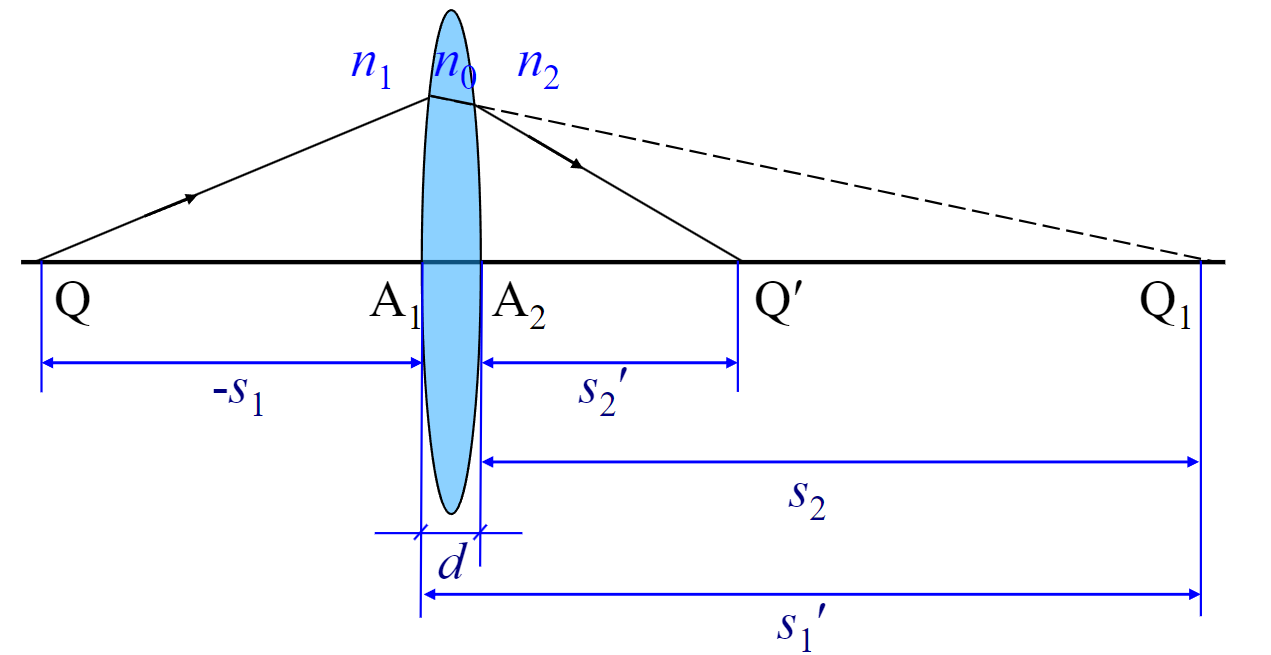
$$
\frac{n_1}{-s_1}+\frac{n_2}{s_2’}=\frac{n_0-n_1}{r_1}+\frac{n_2-n_0}{r_2}\equiv \Phi
$$

透镜公式

焦平面

焦平面（Focal plane）：垂直于光轴且经过焦点的平面

前焦平面（front focal plane）：光射入透镜的面

后焦平面（back focal plane）：光从透镜射出的面

透镜使得光的落点与入射角有关，且满足
$$
y=f \cdot \tan\theta \approx f\cdot \theta
$$
落点

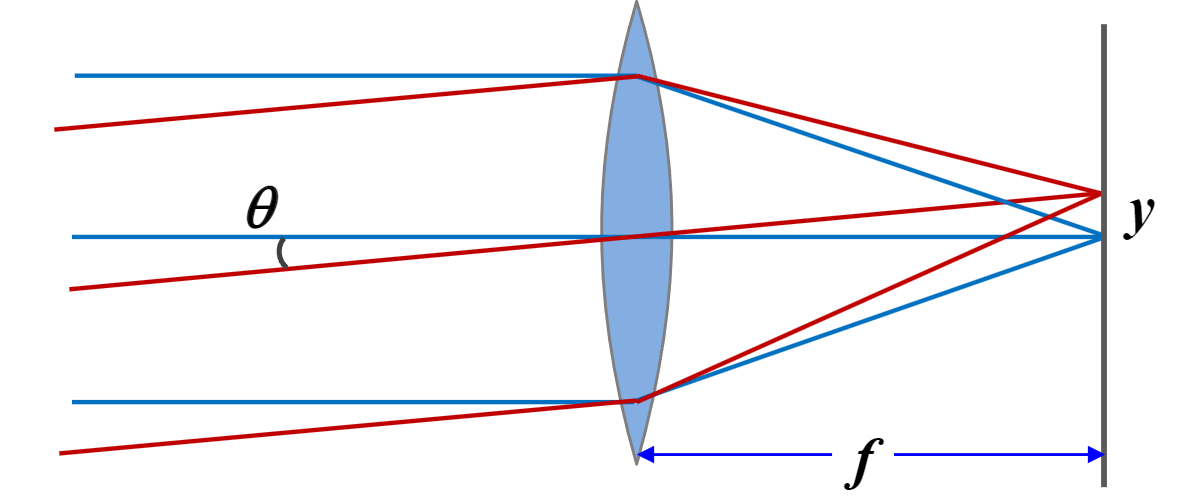
用透镜成像等于两倍的傅里叶变换

光阑

光阑（stop）：限制（limit）成像光束的器件，比如透镜（lens）、光圈（aperture）、窗口片（the frame of windows）

光圈

光圈（aperture stop，下图DD’）：用于限制光线宽度的期间

光圈

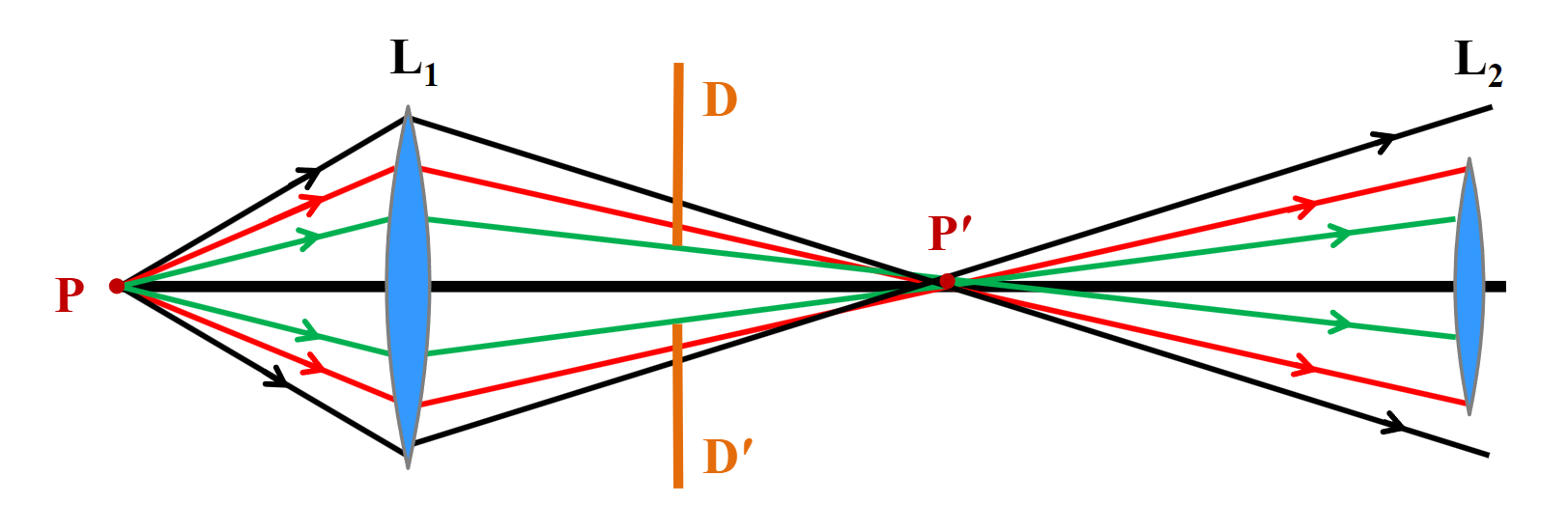
Field stop：用于限制成像区域和方位

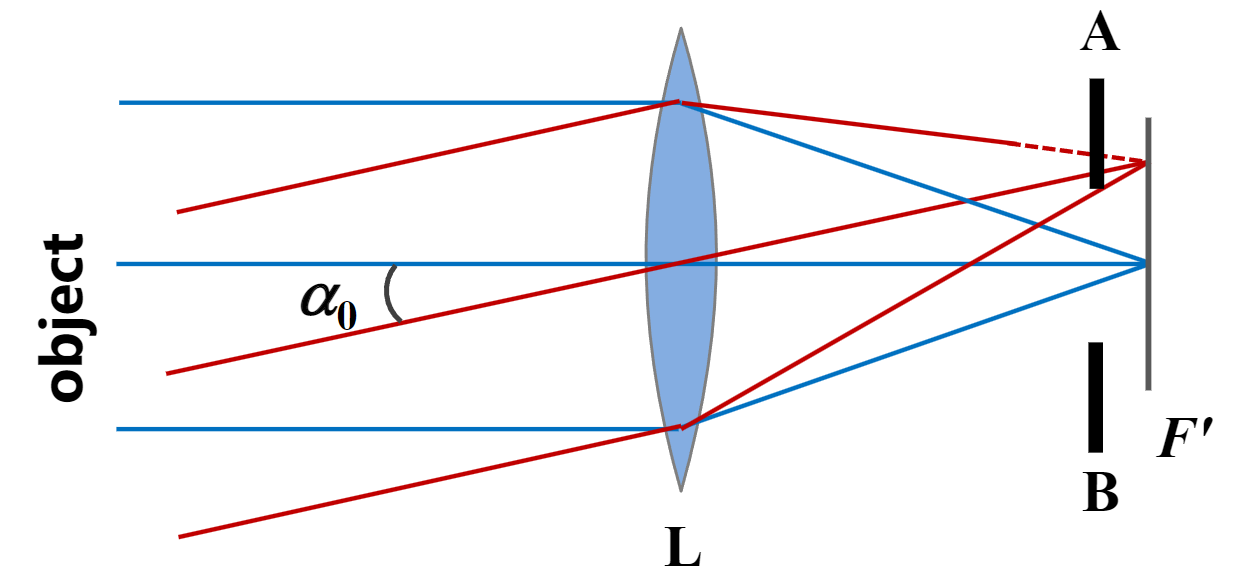
field-stop

景深

景深（Depth of field/focus）：聚焦深度，入射点P在光轴方向移动，移动距离$\Delta x$在景深范围内，图像是清晰的

景深

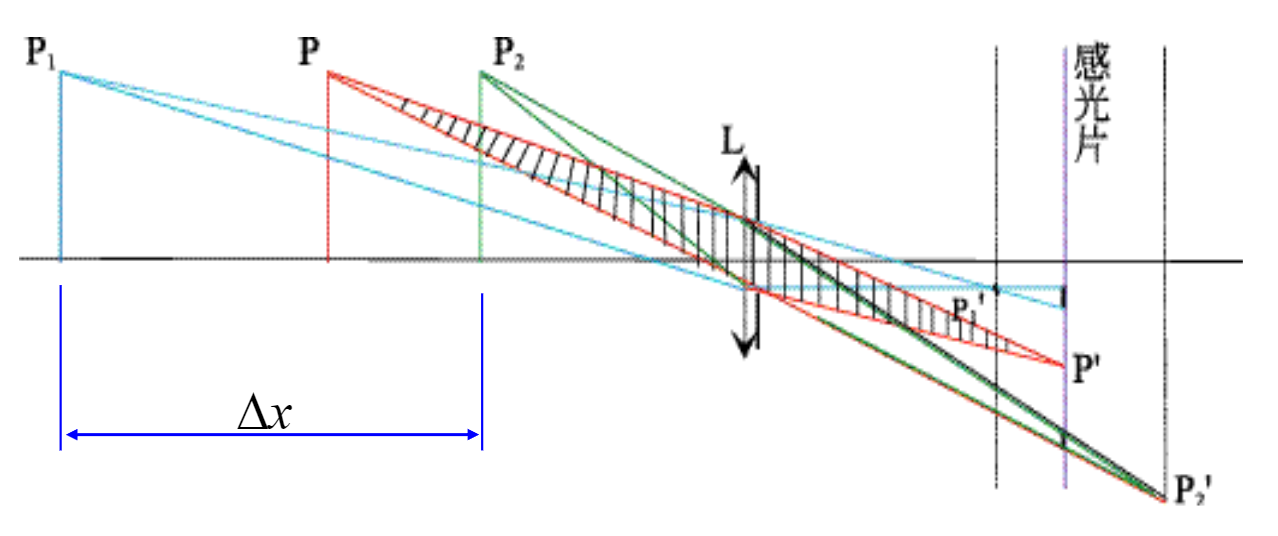
能看出图中$P_1$过早聚焦，$P_2$过晚聚焦，他们相对于$P$，都显得比较模糊

在物体空间的最大$\Delta x$被称为Depth of field

在图像空间的最大$\Delta x$被称为Depth of focus

相对孔径

相对孔径（Relative aperture）：光圈的直径（用$D$表示）和焦距（focal length，用$f$表示）的比值

$D/f$越大，说明光学系统收集光的能力越强

f-number

相对孔径的倒数，意义为焦距是直径的多少倍

比如一个光学系统，焦距160nm，光圈直径20nm，那么它的f-number等于160/20=8，记作$f/8$

更新于：2024年11月18日

光学

评论