光学复习
复习重点
- [x] 相速度
- [x] 偏振态
- [x] 费马原理
- [x] 横向放大率
- [x] 薄透镜成像
- [ ] 透镜组成像(做图法)
- [ ] 反射过程中的相移
- [ ] 布鲁斯特角
- [ ] 反射光与折射光的偏振态
- [x] 全反射
- [x] 相干条件
- [x] 杨氏双缝干涉
- [x] 时间、空间相干性
- [x] 等倾干涉
- [x] 等厚干涉
- [ ] 迈克尔逊干涉仪
- [ ] 多光束干涉
- [x] 增反膜与增透膜
- [x] 惠更斯-菲涅尔原理
- [x] 衍射的分类
- [ ] 衍射与傅立叶变换
- [ ] 单缝衍射
- [x] 圆孔衍射
- [ ] Airy斑
- [ ] 瑞丽判据
- [ ] 多缝衍射
- [x] 光栅方程
- [ ] Abbe成像原理
- [ ] 最小分辨距离、角度
- [x] 光栅
- [x] 双折射
- [x] 惠更斯作图法
- [ ] 波片
- [x] 光偏振态的改变与检测
- [x] 黑体辐射与光量子
作业解析
3.32
一个4.0 v白炽手电筒灯泡消耗0.25 A,将约1.0%的耗散功率转化为光(λ≈550 nm)。如果梁的截面积是10平方厘米,近似圆柱形
(a)每秒发射多少光子?(b)每米光束中有多少光子?©光束离开手电筒时的通量密度是多少?
a
根据功率和光的能量公式
$$
P=UI
$$
$$
n\hslash c/\lambda=0.01P
$$
求出n
b
每米光子数=光子总数/长度
$$
nt=ct
$$
$$
c=3.0\times 10^8
$$
c
$$
密度=0.01P/S
$$
8.4
描述下列光的偏振态
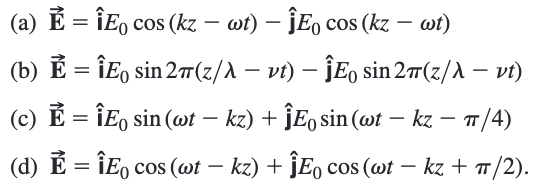
根据xy的振幅和相位判断偏振态
$$
\delta=(E_x/E_y)\Delta \varphi
$$
ab
$$
E_x/E_y=-1
$$
$$
phase(E_x)=phase(E_y)
$$
偏振方向为
$$
-\pi/4
$$
c
$$
E_x/E_y=1
$$
$$
phase(E_x)=phase(E_y)+\pi/4
$$
偏振方向为
$$
\pi/4
$$
d
$$
E_x/E_y=1
$$
$$
phase(E_x)=phase(E_y)-\pi/2
$$
偏振方向为
$$
-\pi/2
$$
记偏振态的技巧
$\delta = 0$时,是一个左下到右上的线偏振,随着$\delta$增大,偏振的形状呈正弦形状,左顺右逆
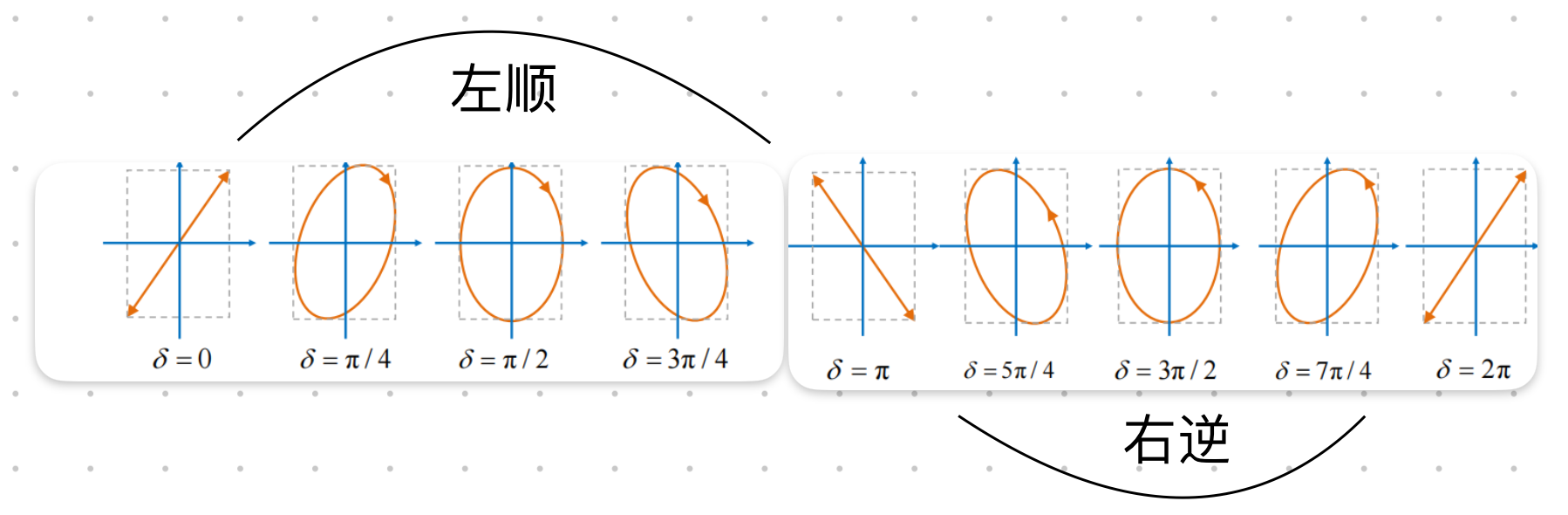
7.36
证明组速度可以写成
$$
v_g=\frac{c}{n}+\frac{\lambda c}{n^2}\frac{\mathrm{d}n}{\mathrm{d}\lambda}
$$
证明
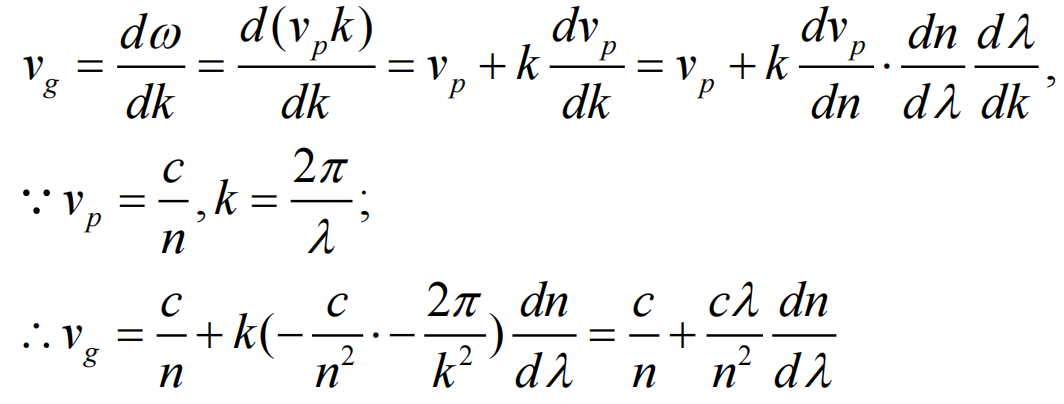
5.5
考试例题
求反射光偏振

- 根据shell公式求折射角
$$
1 \times \sin \theta = n\sin \gamma
$$
$$
\gamma = 18.7^{\circ}
$$
- 根据菲涅尔公式求出反射光ps偏振比
$$
r_p=\frac{\tan (\alpha - \gamma)}{\tan (\alpha + \gamma)}=0.176
$$
$$
r_s=-\frac{\sin (\alpha - \gamma)}{\sin (\alpha + \gamma)}=-0.261
$$
- 得到反射光ps分量
$$
E_p=r_pE_0\cos 45^\circ
$$
$$
E_s=r_sE_0\sin 45^\circ
$$
- 求反射光的偏振和入射面的夹角$\theta’$
$$
\theta’=\arctan|\frac{r_s}{r_p}|=\arctan 1.483=56^\circ
$$
- 由于入射角小于布鲁斯特角
$$
\alpha_B = \arctan n=57.3^\circ
$$
所以ps都有相位移,合成后仍在13象限



