法线切线次切线的计算
顶点法线的计算
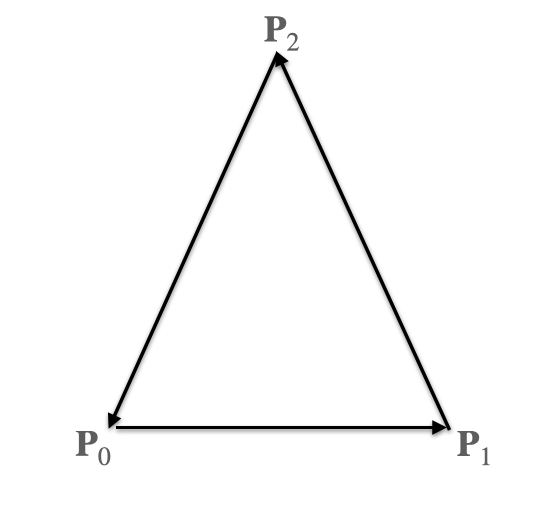
模型顶点构成了多个三角面,使用三角面的顶点坐标等得到两条边的向量,求两个向量的叉积能够得到(归一化的)面法线。
$$
\mathbf{N}=\frac{(\mathbf{P}_1-\mathbf{P}_0)\times(\mathbf{P}_2-\mathbf{P}_0)}{||(\mathbf{P}_1-\mathbf{P}_0)\times(\mathbf{P}_2-\mathbf{P}_0)||}
$$
点的顺序与法线方向满足右手螺旋定则,点呈顺逆时针时法线垂直直面向外。
顶点法线可以在DCC中手动指定,也可以用面法线做平滑着色。一般来说某个顶点会参与构成多个三角面,选取这些三角面的面法线做算术平均值,这个过程被称为平滑着色。
硬边上的点属于不同的平滑组,在计算法线时不能平均,在导出时会被拆分为互相重叠的点,各自拥有一个法线、纹理坐标。
如果对未经过归一化的面法线求均值,能实现含权重的顶点法线,三角面面积越大,影响越强。
切线空间
为了得到更高精度的法线,我们会使用切线空间的法线贴图,对顶点法线进行扰动。
切线空间由三个基向量组成,分别为切线$X$、次切线$Y$、法线$Z$,这三个基向量不一定正交,但视为正交。
在不进行扰动时,切线空间的法线为$(0,0,1)$,是顶点法线的方向。切线和次切线所形成的平面与物体表面相切,方向与UV有关,但存在偏差。
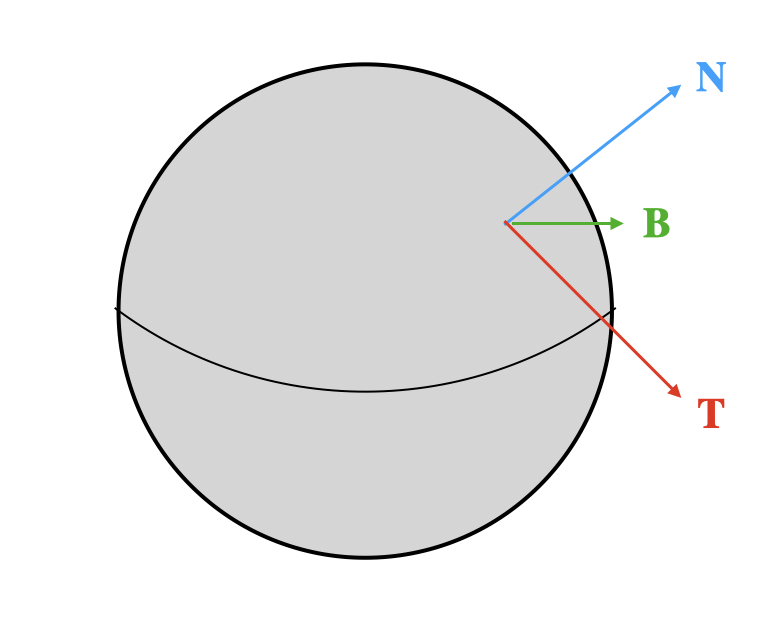
三个向量可以构成TBN矩阵,该矩阵能将切线空间法线转化为物体空间/世界空间
$$
\begin{bmatrix}T_{x}&B_{x}&N_{x}\\ T_{y}&B_{y}&N_{y}\\ T_{z}&B_{z}&N_{z}\end{bmatrix}
$$
float3 normalValue = normalTexture.sample(textureSampler, uv * params.tiling).xyz * 2.0 - 1.0;
normal = float3x3(tangentWS, bitangentWS, normalWS) * normalValue;
|
计算切线和次切线
int triangleCount = indices.Count / 3;
List<float3> sDirList;
List<float3> tDirList;
for(int i = 0; i < triangleCountl; ++i){
int vertexID0 = indices[i * 3];
int vertexID1 = indices[i * 3 + 1];
int vertexID2 = indices[i * 3 + 1];
float2 uv0 = uvs[vertexID0];
float2 uv1 = uvs[vertexID1];
float2 uv2 = uvs[vertexID2];
float3 pos0 = positions[vertexID0];
float3 pos1 = positions[vertexID1];
float3 pos2 = positions[vertexID2];
float2 s = float2(uv1.x - uv0.x, uv2.x - uv0.x);
float2 t = float2(uv1.y - uv0.y, uv2.y - uv0.y);
float3 deltaPos0 = pos1 - pos0;
float3 deltaPos1 = pos2 - pos0;
float r = 1.0f / (s.x * t.y - s.y * t.x);
float3 sDir = float3(
r* (t.y * deltaPos0.x - t.x * deltaPos1.x),
r* (t.y * deltaPos0.y - t.x * deltaPos1.y),
r* (t.y * deltaPos0.z - t.x * deltaPos1.z)
);
float3 tDir = float3(
r* (-s.y * deltaPos0.x + s.x * deltaPos1.x),
r* (-s.y * deltaPos0.y + s.x * deltaPos1.y),
r* (-s.y * deltaPos0.z + s.x * deltaPos1.z)
);
tDirList[vertexID0] += tDir;
tDirList[vertexID1] += tDir;
tDirList[vertexID2] += tDir;
sDirList[vertexID0] += sDir;
sDirList[vertexID1] += sDir;
sDirList[vertexID2] += sDir;
}
for(int i = 0; i < vertexCount; ++i){
float3 normal = normals[vertexID0];
float3 tDir = tDirList[i];
float3 tangent = tDir - dot(normal, tDir);
float3 bitangent = cross(normal, tangent);
}
|
参考
切线空间(Tangent Space)完全解析
《3D游戏与计算机图形学中的数学方法》





