SPH入门
SPH(Smoothed Particle Hydrodynamics)光滑粒子流体力学
A mesh-free method for the discretization of functions and partial differential operators
SPH是一种基于拉格朗日视角的算法,是一种空间离散化的算法,常用于连续介质的数值模拟
-
材质导数的坐标
-
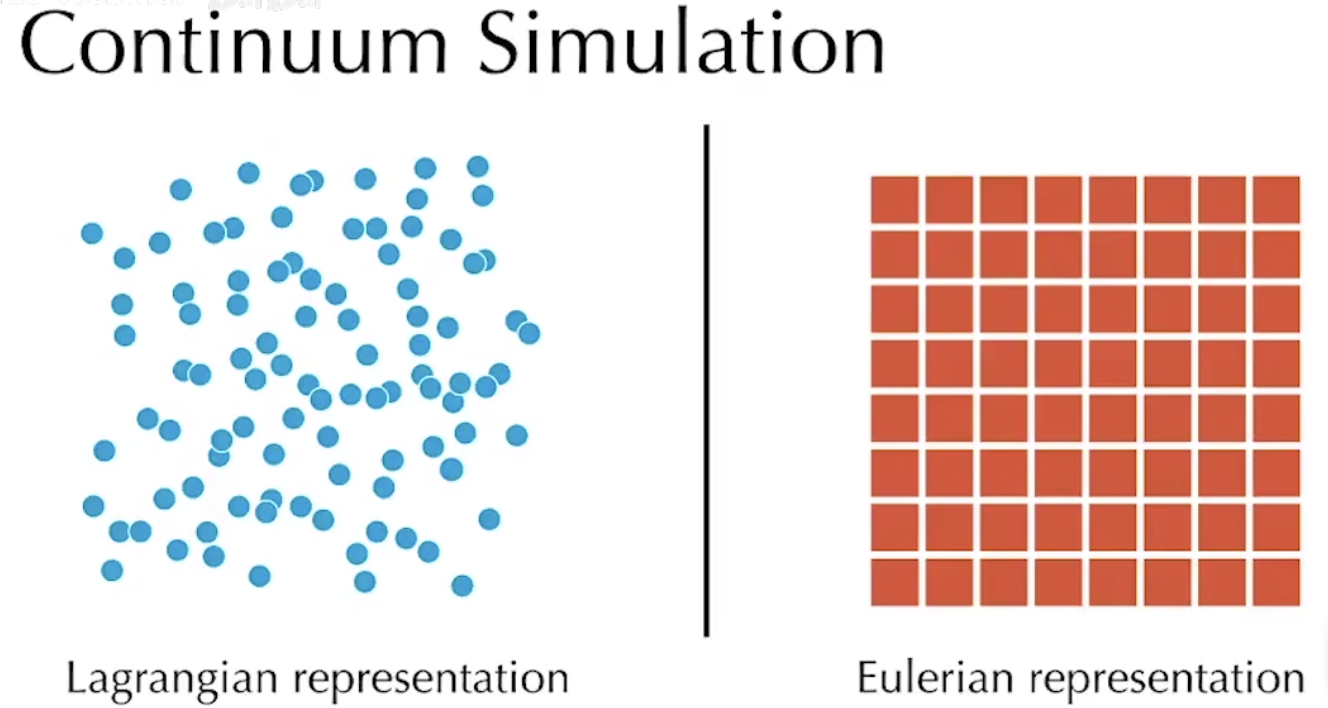
拉格朗日坐标:视角随着介质移动而移动(粒子模拟)
-
欧拉坐标:视角是固定的,检测穿过视角的介质流速(网格模拟)
-
SPH进行简单流体模拟,简单来说就是
- 介质离散化,使用多个质点来表示流体(离散化)
- 对于每一个粒子,找到它附近的粒子(临域搜索)
- 计算密度(质量密度估计)
- 计算压强(控制方程,如理想气体状态方程+动量守恒),压强差、粘滞力等
- 更新运动状态
- 水体渲染(Marching Cube)
离散化
狄拉克函数
狄拉克$\delta$函数,这是一个广义函数,其在整个定义域中积分值都集中在原点
$$
\delta (\mathbf{r})= \begin{cases}
\infty & |\mathbf{r}|=0 \\
0 & otherwise
\end{cases}
$$
该函数仅在积分中有意义,可以通过高斯钟形函数(正态分布)逼近
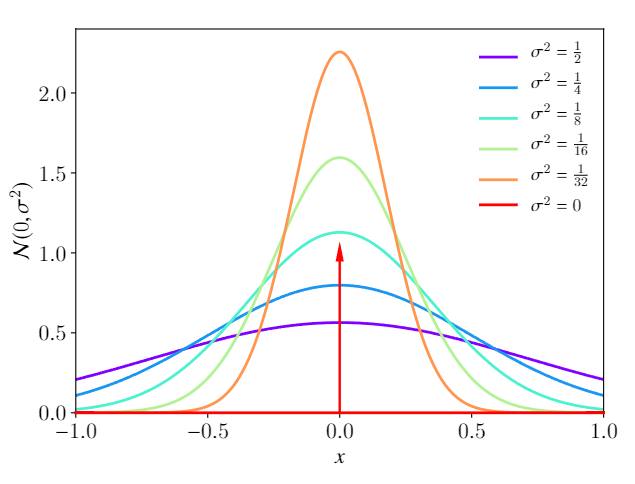
在物理学中我们常用质点表示物体,但是因此使得密度函数失去了意义(因为质点没有空间),此时密度函数就塌缩成了狄拉克函数
空间中任何标量场函数,都可以用狄拉克函数表示:
$$
A(\mathbf{x})=(A*\delta)(\mathbf{x})=\int A(\mathbf{x}‘)\delta (\mathbf{x}-\mathbf{x}’)dv’
$$
- $dv’$是$\mathbf{x}'$对应的体积积分变量
- $A(\mathbf{x}): \mathbb{R}^d \rightarrow \mathbb{R}$,d是维度,意思就是这是一个空间函数
$\mathbb{R}$是实数集
$\mathbb{R}^+$是正实数集(不含0)
$\mathbb{R}^d$是d维实数集
光滑核函数
我们有了狄拉克函数,想要把连续函数来离散表示
核函数(kernel functions,smoothing kernels)是一种随着距离而衰减的函数,与高斯函数要在整个作用域积分不同,核函数是有最大影响半径的,最大影响半径用$h$表示
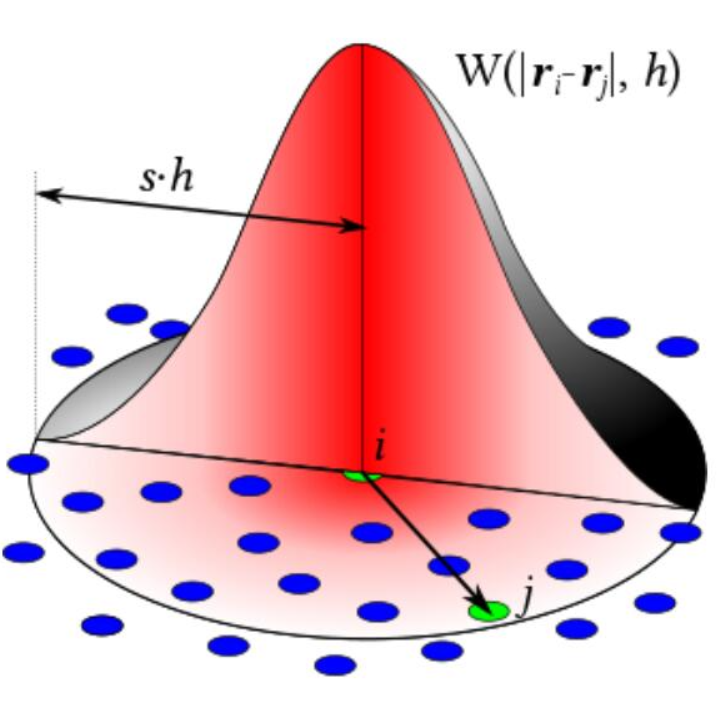
核函数满足
- 归一化
- 狄拉克条件
- 非负性
- 对称性
- 有界性
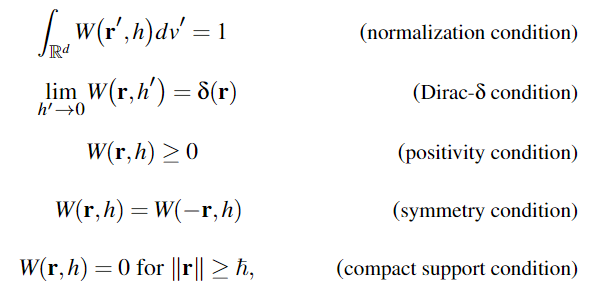
一个经典的核函数是三次样条器(cubic spline kernel)
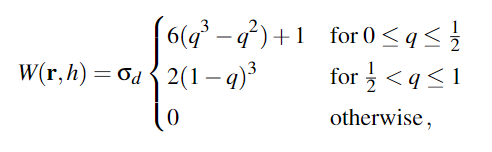
- 其中$q=\frac{1}{h}||\mathbf{r}||$
离散化
有个数学大佬告诉我,这里就是“在某个i点处求所有其他j点按核函数加权的平均值,只不过离散化的时候划成了区块赋予了密度和体积”
换句话说,这其实就是一次卷积(数学家真是不讲人话)
参考上面那张核函数的图,离散化就是对于$i$点,我们求该点附近场密度函数值和核函数(一堆$j$点)的加权平均值
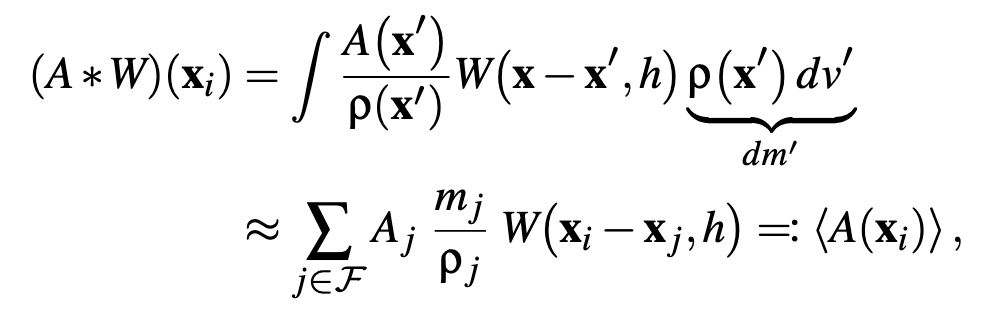
在数学上,$\langle A(x)\rangle $表示平均值
质量密度估计
粒子不需要携带质量密度函数,对于空间中任意位置的点,都可以通过离散化求出该点密度
对于$\mathbf{x}_i$位置处的点,其密度为:
$$
\rho_{i} =\sum_{j} m_{j}W_{ij}
$$
不过在流体边界,这样求密度会导致数据偏小,需要做边界处理
下图绿色点临域完整,得到正确的密度,而红色点只能得到一个较小的密度
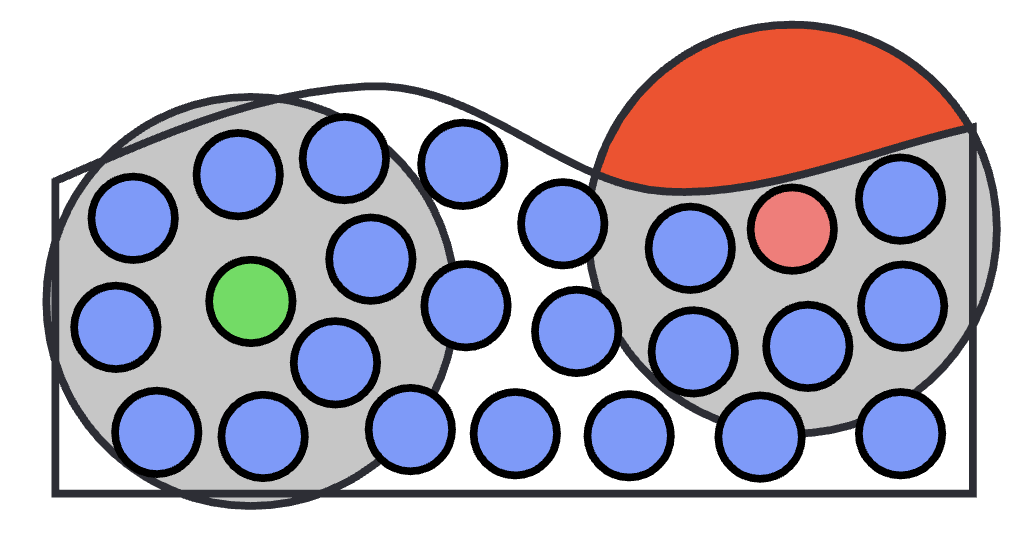
微分算子的离散化
上面我们已经实现场函数的离散化,实现了质量密度估计。但除此之外,还有一些空间微分算子(导数)值得离散化
$$
\nabla A_{i}\approx \sum_{j} A_{j}\frac{m_{j}}{\rho_{j} } \nabla W_{ij}
$$
关于拉普拉斯算符,可以去看Nabla算子,简单来说这东西是将标量场转化为向量场,一阶算符就是梯度,二阶是散度,用于得到数据变化最快的方向。文中也实现了拉普拉斯算符的离散化
文章介绍了两种最常用的梯度的近似方法,并给了适用范围
- 差分公式(Difference Formula):用于近似速度的散度
- 对称公式(Symmetric Formula):用于近似力、脉冲的梯度
差分公式
在高中学微积分时,我们用两个相邻的点组成的线来逼近切线,以此引入了极限、导数的概念。在实际应用中,这两个点不可能无穷近,于是存在误差
使用差分表示导数(导数就是),我们只能把$h$取到一个很小的值,而不是无穷小,因此这个导数是有误差的
$$
f’(x)=\lim_{h \rightarrow0}\frac{f(x+h/2)-f(x-h/2)}{h}
$$
我们需要衡量这个误差的大小,于是我们将$f(x\pm h/2)$泰勒展开后带入上式,得到
$$
f’(x)=\lim_{h \rightarrow0}\frac{f’(x)h+O(h^3)}{h}=f’(x)+O(h^2)
$$
误差大小为$O(h^2)$
经计算,二阶导数的误差也是$O(h^2)$
对称公式
临域搜索
这里介绍最简单的,不做空间优化的临域搜索,进阶内容可以看临域搜索
由于核函数存在作用范围,我们在积分时,只需要遍历核半径内其他粒子的信息。这样相较于nxn的全遍历,能大幅减少计算,为此我们需要构建临域表
网格化
临域搜索是一种基于网格(grid)构建粒子拓扑关系的算法,找到该粒子所在位置和其相邻位置有哪些粒子
我们将整个(粒子作用的)场景均匀切分为一个个三维网格,每个网格为立方体,边长等于核半径$\hslash $,
每个网格拥有一个坐标$(i,j,k)$,用于表示网格在场景中的位置
对于任意一个粒子,其核函数的作用范围是一个球,临域搜索就是计算球内有哪些粒子
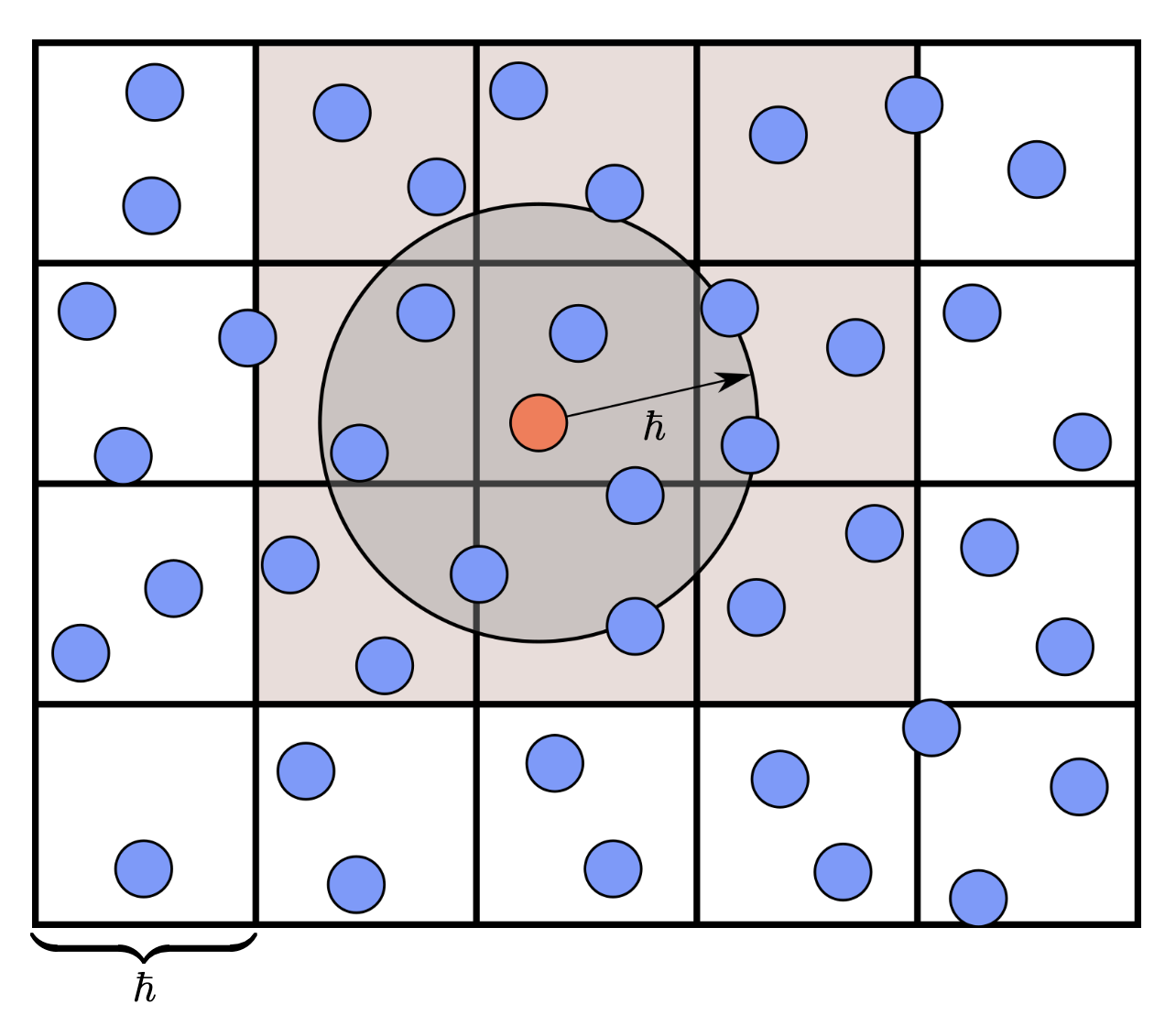
- 空间网格化
- 遍历粒子,记录每个网格中有多少个粒子,有哪些粒子
- 遍历粒子,建立临域表
- 求该粒子的核函数球位于哪些网格中
- 遍历那些网格,取出网格中所有粒子,计算距离
- 将距离小于核半径的粒子id存储在临域表中
数据结构
| 名称 | Key | Value |
|---|---|---|
| _neighbourList | id.x * maximumParticlesPerCell * 8 + _neighbourTracker[id.x]++ | 临居的id |
| _neighbourTracker | id.x | 当前粒子有多少个临居 |
| _hashGrid | hashCellIdx * maximumParticlesPerCell + previousCount | id.x |
| _hashGridTracker | hashCellIdx | 该网格中的粒子数 |
- id.x:当前粒子id
- hashCellIdx:网格坐标的Hash值
- maximumParticlesPerCell:每个网格的的粒子最大数量(提前留好空)
- previousCount:空里有几个粒子
球作用于哪些网格
我们发现核函数球最少位于8个网格中(一个2x2x2的立方体),最多位于27个网格中(一个3x3x3的立方体),我们只需要找出核函数球位于哪些网格中,就能减少很多便利
在这里,我们只使用8个网格作为临域(舍弃那些不重要的网格),很显然,球心向哪个方向靠,我们就使用哪8个网格
- 找到球心所在网格坐标,构建临域坐标表,临域坐标初始均设为球心位置
- 判断中心网格的中心坐标与球心的坐标位置关系
- 存储临域Hash Key
void GetNearbyKeys(int3 originIndex, float3 position, out int nearbyKeys[8]) |
构建临域表
[numthreads(100, 1, 1)] |
控制方程
尽管物体在微观层面(比如原子)是离散的,但在宏观层面上,流体、固体表现为连续介质
continuum, a region of continuously distributed mass
根据定义,一个连续介质可以被切分为多个小的连续介质(类比实数的稠密性,任意两个实数间总存在第三个实数),而不影响其性质
材料粒子(material particle):a portion of matter contained in an infinitesimal volume
连续性方程
连续性方程描述了物体的密度与时间的关系
$$
\frac{D\rho}{Dt}=-\rho(\nabla \cdot \mathbf{v})
$$
随体导数
随体导数(material derivative):$\frac{D(\cdot)}{Dt}$
随体导数描述了材质点的场量随着时间的变化率
在制作不可压缩的介质中,必须始终保持
$$
\frac{D\rho}{Dt}=0
$$
随体导数与坐标系有关,常见的坐标系有:拉格朗日坐标系和欧拉坐标系
线性动量守恒定律
高中物理就学过的碰撞时动量守恒,力作用在物体上,会改变物体的动量
将运动公式(equation of motion)用积分的形式写出来就是
$$
\rho \frac{D^2\mathbf{x}}{Dt^2}=\nabla \cdot \mathbf{T}+\mathbf{f}_{ext}
$$
- $\mathbf{T}$:应力张量(stress tensor)
- $\mathbf{f}_{ext}$:体积力(body forces),穿越空间作用在所有流体元上的非接触力,例如重力、惯性力、电磁力
理解应力张量
对于材质内部一个微小平面,这个平面会受材质中其他点的作用力,这个力可能不与平面垂直。其中垂直于平面的力叫正向应力,平行于平面的力叫剪应力
矢量是一种一维张量,由大小和一个方向组成。然而对于应力,我们没法使用矢量进行表示,于是改用二维张量来表示,一个方向是应力的指向,一个方向是应力所在的平面方向
对于材质内一个点,它可能处于无数个平面中,我们需要用一种平面无关的方式来表示其受力状态。在三维空间中,我们选择了三组正交基底$(\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3)$构建坐标系,应用中给定一个方向$\mathbf{e}$,就能求出该方向的应力矢量
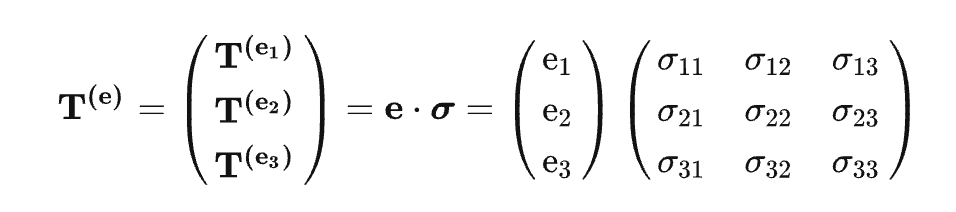
其中$\mathbf{T}$为应力矢量,$\sigma $为柯西应力张量(一个3x3的矩阵)
$\sigma_{xy}$的意思是,处于yz平面,指向y方向
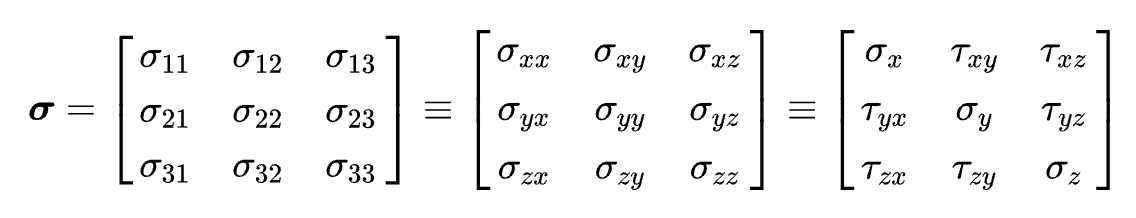
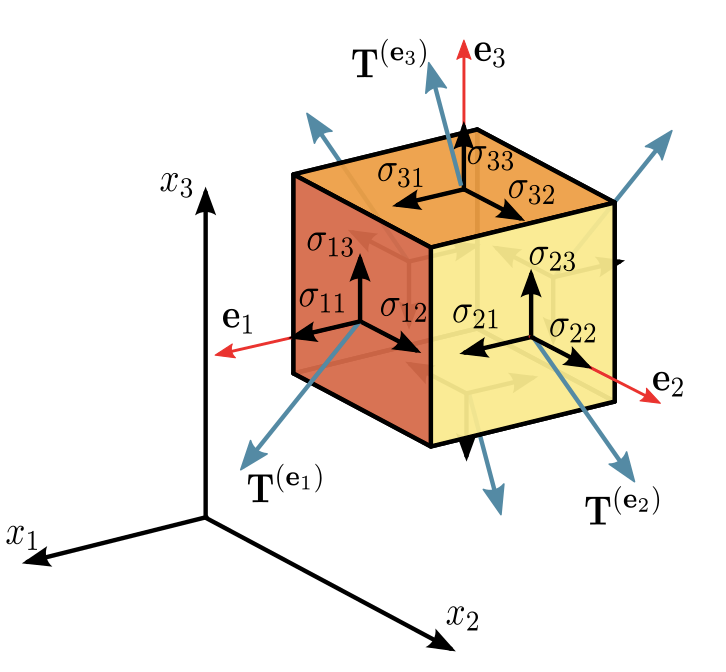
柯西应力张量只适用于材料微小变形的情况
Navier-Stokes方程
一个经典的不可压缩流体的张力表示方法
$$
\mathbf{T}=-p+\mu (\nabla \mathbf{v}+\nabla \mathbf{v}^T)
$$
- $p$:压强
- $\mu$:粘度(viscosity )
我们将该液体的应力张量公式带入牛顿运动公式,得到速度的公式
$$
\rho \frac{D\mathbf{v}}{Dt}=-\nabla p + \mu \nabla^2 \mathbf{v}+\mathbf{f}_{ext}
$$
压强可以由密度表示,根据理想气体压强公式,我们得知压强与密度呈线性关系,于是我们取一个静止状态下的密度$\rho_0$,通过与当前状态密度做差值,就能得出压强
理想气体压强公式,初中就学了,$pV=nRT$
$$
p=B((\frac{\rho}{\rho_0})^{\gamma}-1)
$$
- $B$:体积模量(bulk modulus)
弹力
拥有弹力的固体,应力张量来自于固体的形变,之后会展开讲
积分求解
混合初始边界值问题
我们上面给出了控制方程,但是想要求解运动问题,必须给定初始位置和速度(场)
一般而言,混合初始边界值问题(Mixed Initial-Boundary Value Problem)没有解析解,只有数值解
得嘞,这一节就这一句话,这一句话一个字都看不懂
混合边界
简单来说,就是要想求解运动问题,必须既要给初始位置,也要给初始速度(场)
边界条件也叫定解条件,是微分方程里的概念,给定初始值才能求控制方程、偏微分方程的解(比如带入解中的未知数)
放在物理学中叫临界条件,就是物体处于某两种状态间的交界处,比如冰水混合物
边界条件对于解决物理问题(比如求极值)十分重要
有三类边界条件
- 第一类边界条件(迪利克雷边界条件,Dirichlet boundary condition)
- 直接告诉你边界值,比如热传递中告诉你边界处温度
- 第二类边界(若依曼边界条件,Neumann boundary condition)
- 告诉你边界处的梯度,比如热传递中告诉你热流密度(温度的梯度)
- 混合边界条件
- 第一二类边界的混合,比如热对流微分公式,公式中既有温度,也有梯度,只有同时给出两者,才能求解
$$
q=h(T_0-T_a)
$$
解析解与数值解
- 解析解(analytic solution),形如一个函数,给定变量就能得出任意位置的解
- 数值解(numerical solution),这是一个数,是采用有限元、数值逼近、插值等方法得到的解
据说在数学家和物理学家眼里,解析解才是真正的解,更高贵,美丽
让我突然想到三体力魏成想要求出三体问题的解析解,结果最后发现这个问题只有数值解
算子分裂
就是使用分治的算法,将一个复杂的偏微分方程(PDE),分解为几个连续的子问题
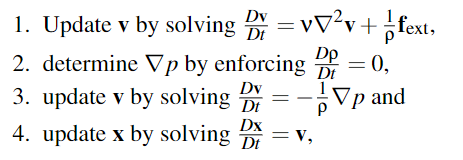
在实践中证明,像这样每步操作依赖于上一步,一步一步操作,能提高系统的稳定性
时间积分
在实时渲染中,和精度相比,性能、稳定性和鲁棒性更重要
在GAMES201开篇讲弹簧质点模型时,关于质点的运动方程,给出了两种积分器:显式积分器和隐式积分器
显式积分器
从过去的状态得到现在的状态,表示简单容易实现
$$
\mathbf{v}_{t+1}=\mathbf{v}_t+\Delta t \frac{\mathbf{f}_t}{m}
$$
$$
\mathbf{x}_{t+1}=\mathbf{x}t+\Delta t \mathbf{v}{t+1}
$$
但是显式积分器有一个问题,就是容易爆炸,于是$\Delta t$不能太大,应满足
$$
\Delta t \le c\sqrt{\frac{m}{k}} \ \ (c \sim 1)
$$
CFL条件
这是CFL条件(Courant–Friedrichs–Lewy condition),是某些偏微分方程的收敛条件,它决定了显式积分器中粒子在单位时间内走过的距离,必须小于粒子大小(或者说质点间的间距)
$$
\Delta t \le \lambda \frac{\tilde{h}}{|\mathbf{v}^{\max}|}
$$
- $\tilde{h}$:粒子大小(质点间的间距)
- $\lambda$:一个常量
- $\mathbf{v}^{\max}$:粒子运动的最快速度
隐式积分器
现在的状态依赖于现在的状态(求$t+1$时刻的信息,结果需要$t+1$时刻的信息),难以实现,但鲁棒性强
$$
\mathbf{v}_{t+1}=\mathbf{v}t+\Delta t \mathbf{M}^{-1}\mathbf{f}(\mathbf{x}{t+1})
$$
$$
\mathbf{x}_{t+1}=\mathbf{x}t+\Delta t \mathbf{v}{t+1}
$$
- $\mathbf{M}$:质量矩阵
Marching Cube
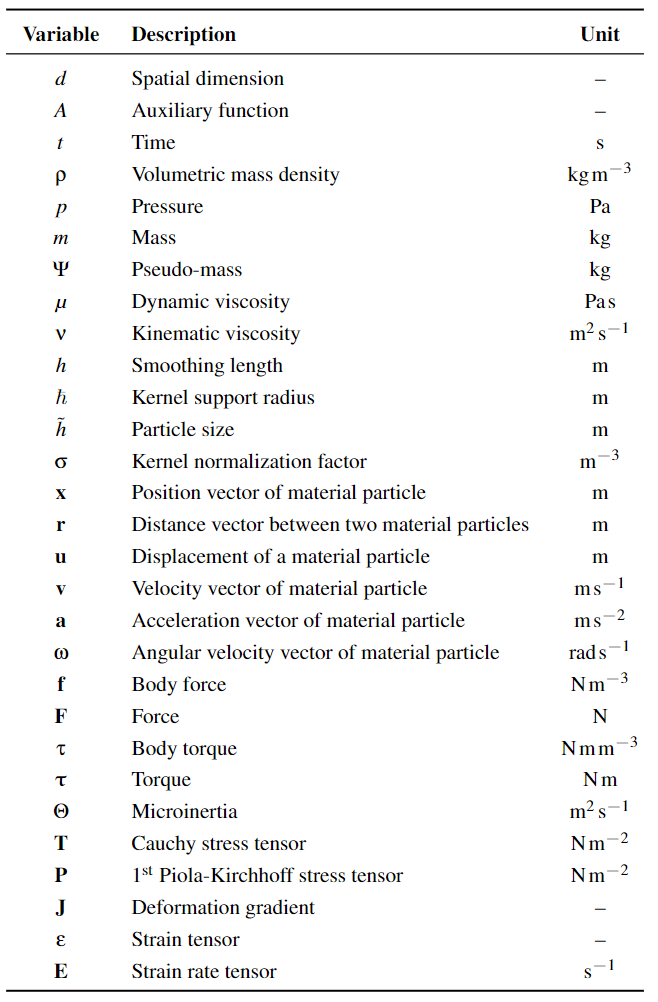
符号表