《Physically Based Shading at Disney》阅读笔记
2012年SIGGRAPH,迪士尼提出了迪士尼规则的基于物理的渲染,立刻成为行业标准,被各大游戏厂商和游戏引擎所采用
本文采用第一人称,我们是指迪士尼
介绍
当时场景渲染还在使用ad-hoc着色模型和punctual灯光,我们渴望一套一致性的、美术友好的着色模型。受毛发渲染启发,我们推出了符合迪士尼规则的PBR模型。
迪士尼PBR模型提供了多种不同的渲染方程,但美术不需要关心渲染的底层逻辑,不需要针对不同的方程调整参数。
微表面模型
BRDF(双向反射分布函数)表示反射光与入射光的能量关系,是某方向出射光辐射率(Radiance)和入射光辐照度(Irradiance)的比值。
微表面模型认为材质表面由无数个理想镜面排列组成,如果某个观察方向上能观察到反射光,那么必然有一些微表面,他们的法线能平分入射光方向和观察方向(几何光学),我们将这些微表面的法线方向称为半向量(half vector)。顾名思义,半向量是入射光和观察方向的一半。
$$
\mathbf{h}=\frac{\mathbf{l}+\mathbf{v}}{|\mathbf{l}+\mathbf{v}|}
$$
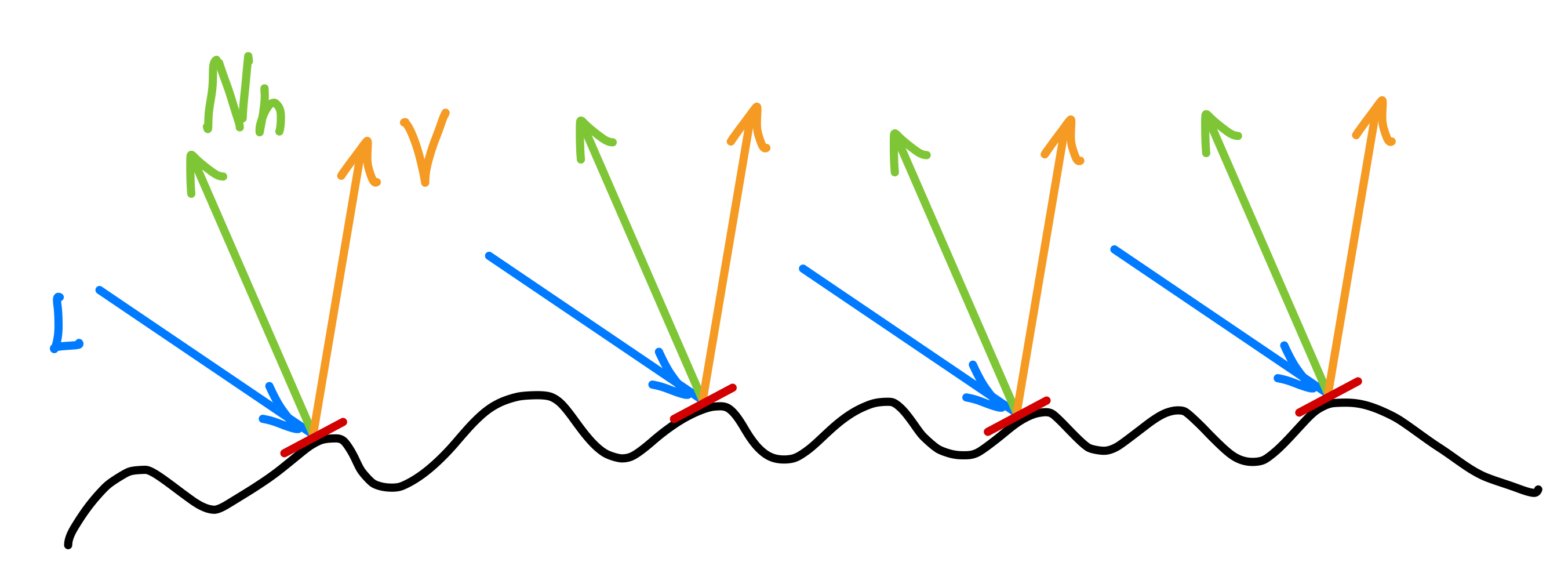
一个各向同性的BRDF模型如下,由菲涅尔项、微表面法线分布项、几何遮挡项组成
$$
\rho\left(\mathbf{l}, \mathbf{v} \right)= \mathrm{diffuse} + \frac{F\left( \theta_d \right) D\left( \theta_h \right) G\left( \theta_l,\theta_v \right) }{ 4\cos\theta_l\cos\theta_v}
$$
- $\theta_d$是入射光和半向量的夹角,d是difference的意思
- $\theta_h$是半向量和法线的夹角
- $\theta_l$是入射光和法线的夹角
- $\theta_v$是观察方向和法线的夹角
BRDF可视化
我们制作了一个BRDF可视化工具,并将扫描材质转化为Image slice
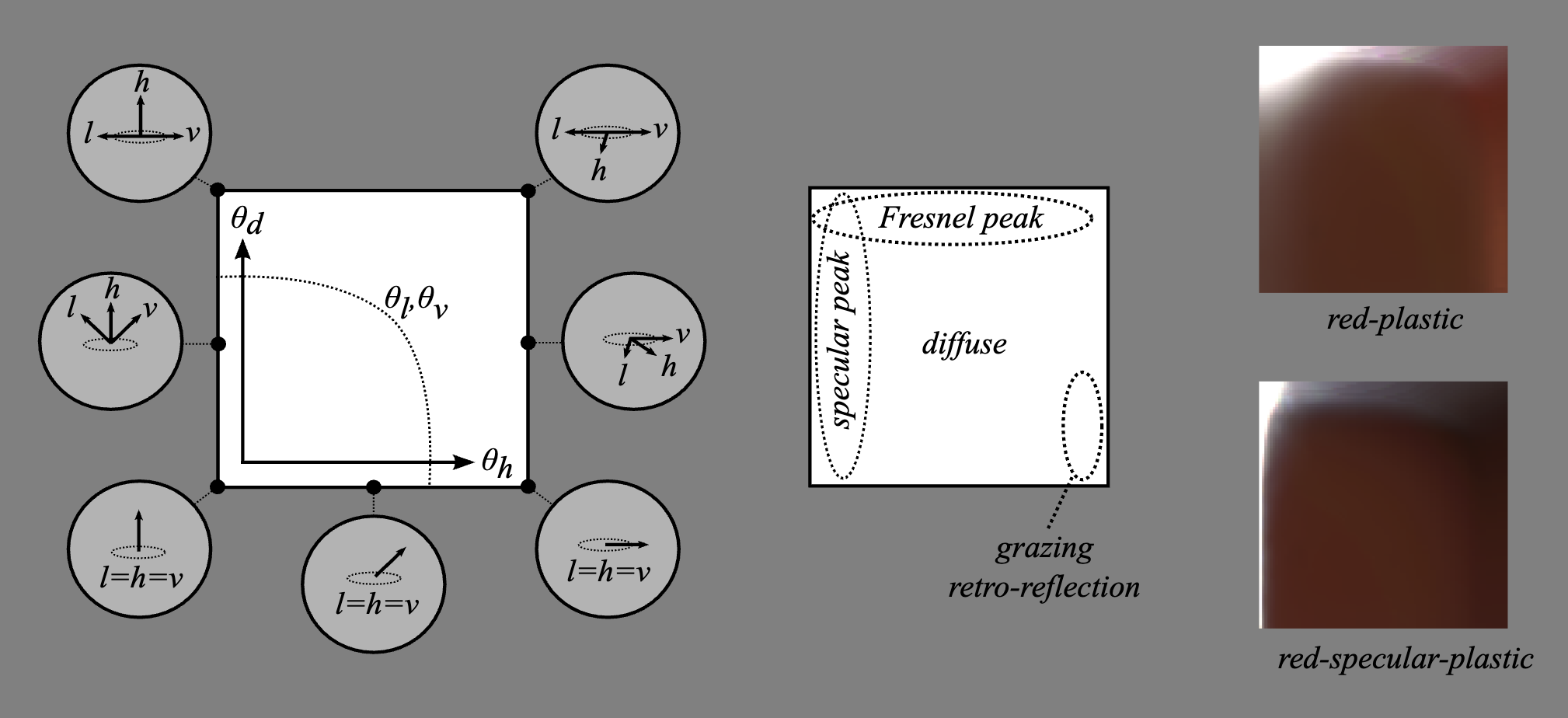
- 在最底侧$\theta_d=0$,入射光和视线重合
- 在最左侧$\theta_h=0$,视线位于反射最强烈的部分,是高光项
- 在最上侧$\theta_d$最大,模拟光线射到材质边缘是的菲涅尔现象
观察材质
漫反射项
漫反射是灯光进入材质后经过折射、散射后重新发散到材质外部的过程。BRDF并没有考虑光线进出材质的位置变化,没有模拟次表面散射。
下图为随着$\theta_h$的增大,反射强度的衰减程度,光滑材质反射强度衰减的极快。而粗糙材质就比较慢,甚至有些材质的反射强度与方向无关。部分粗糙材质在掠射角有菲涅尔现象
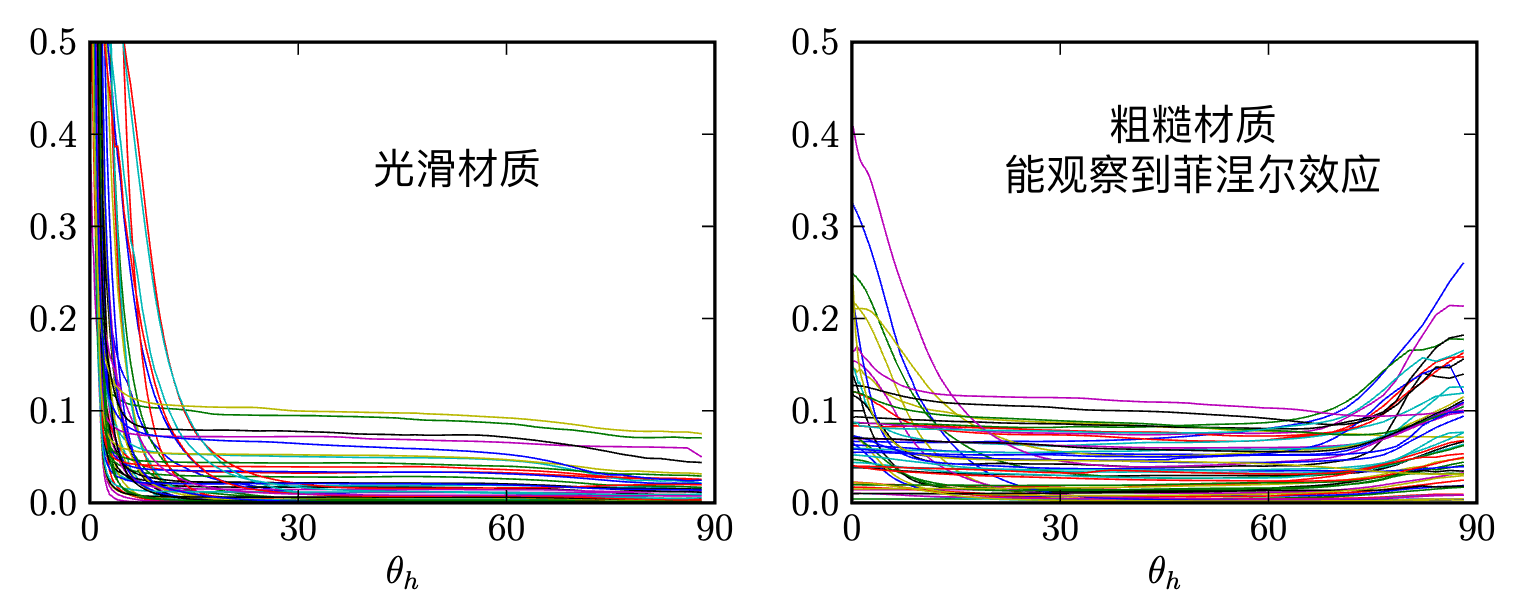
微表面理论认为材质表面由大量理想镜面组成,光线呈掠射角入射时,入射光线与模型边缘的一些“竖直的”微表面相遇,使许多光发生了反射,形成了菲涅尔效应,更多的能量被用于反射,而非散射。
微表面法线分布项
微表面项描述了沿着半向量方向的微表面占总面积的比例。对于光滑材质,大多数微表面法线与宏观法线方向一致,随着$\theta_h$增大,面积会迅速减少,而粗糙材质减少就很慢,有着更长的尾部。
下图左为GGX(红)、Beckmann(绿)、Blinn Phong(蓝,注意和绿重叠了)、chrome(黑)四种D项的描述,右图从左到右分别为点光照射chrome、GGX、Beckmann项的结果。

高光菲涅尔项
菲涅尔项描述了光线发生反射和折射的比例,当光线由光疏材质射向光密材质时,随着入射角的增大,反射会越来越强。对于光滑材质,掠射角时菲涅尔项接近100%,对于粗糙材质,尽管无法达到100%,但也增长迅速。
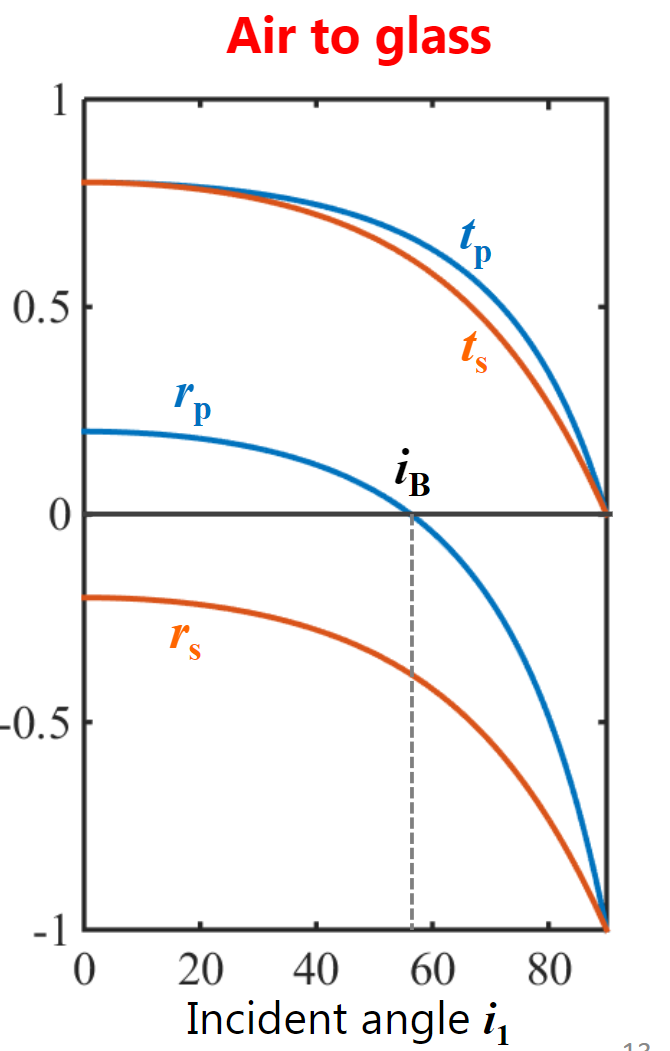
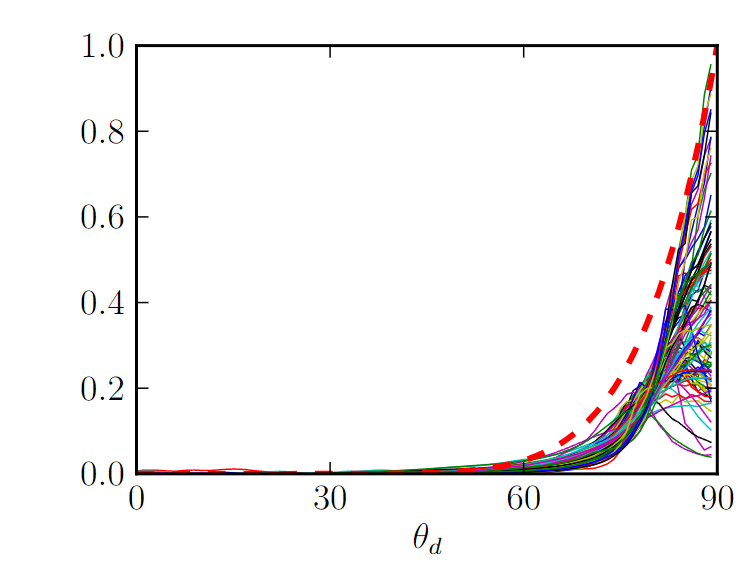
人们发现有些材质的菲涅尔曲线在掠射角处比菲尼尔方程预测的更陡峭,为此引入了几何遮挡项,该项将方法菲涅尔效应。
几何遮挡项
实践中难以测量出几何遮挡项,于是是通过先测量出F项和D项,再计算出G项。
Smith根据D项推导出了一种G项,不过Smith的G项仅再某些情况下有解析式,大部分情况下使用预积分+图表的方式近似。
迪士尼BRDF
材质参数
参数直观、数量少,参数范围通常在0~1但允许超出范围,所有参数组合都是鲁棒合理的
| 参数名称 | 含义 |
|---|---|
| baseColor | 基础色 |
| subsurface | 通过次表面控制漫反射形状 |
| metallic | 金属度,所有材质是金属和非电介质根据金属度的混合,0为非金属,1为金属 |
| specular | incident specular amount. This is in lieu of an explicit index-of-refraction |
| specularTint | 美术可以通过该参数将高光色调向基础色 |
| roughness | 粗糙度 |
| anisotropic | 各项异性比,用于控制高光形状,0为各项同性,1为各项异性 |
| sheen | 光泽,用于布料渲染 |
| sheenTint | 美术可以通过该参数将光泽调向基础色 |
| clearcoat | 薄膜图层的高光色 |
| clearcoatGloss | 薄膜图层的粗糙度 |

漫反射模型
漫反射的本质是光线进入材质后重新射出,因此至少发生了两次折射,于是有两个菲涅尔项。这两个菲涅尔还能让材质边缘变亮。
$$
\rho_d=\frac{baseColor}{\pi}(1+(F_{D90}-1)(1-\cos \theta_l)^5)(1+(F_{D90}-1)(1-\cos \theta_v)^5)
$$
$$
F_{D90}=0.5+2roughness\cos^2\theta_d
$$
高光D项
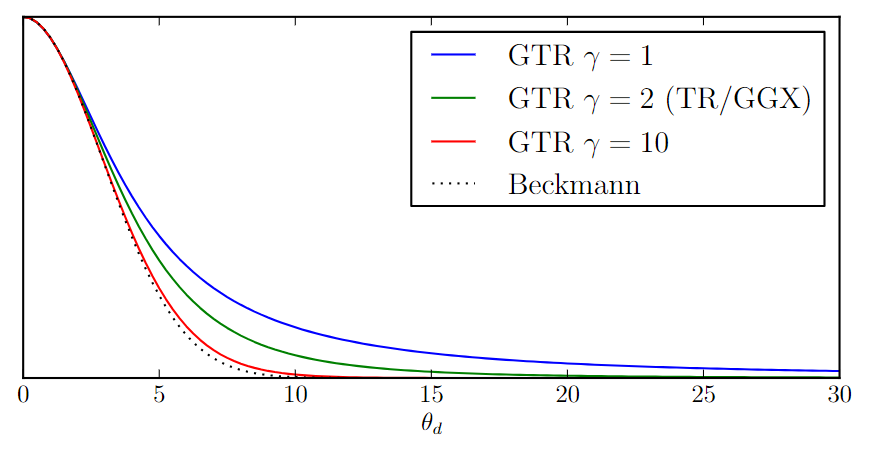
我们认为目前最流行的GGX拖尾仍不够长,最后选择了GTR
$$
D_{GTR}=c/(\alpha^2\cos^2\theta_h+\sin^2\theta_h)^{\gamma}
$$
- $c$:缩放常数
- $\alpha$:粗糙度参数,0为光滑,1为完全粗糙
高光F项
$$
F_{\mathrm{Schlick}}=F_0+(1-F_0)(1-\cos\theta_d)^5
$$
高光G项
使用GGX模型作为G项,但对粗糙度进行映射
$$
\alpha_g=(0.5+roughness/2)^2
$$



