ResNet
当时,难以训练更深的神经网络,为此作者提出了一个残差(residual)学习框架,用于简化网络的训练。最终取得了惊人的效果,和当时很多工作比,具有更少的参数和更深的网络,甚至能达到千层
退化现象
深度神经网络在图像分类上取得了一系列巨大突破(AlexNet、VGGNet),他们的成功还表明模型深度对效果的影响非常大,通过标准初始化、中间标准化层的方法解决了梯度爆炸/消失的问题,现在已经可以训练十多层的模型,但难以训练更深的模型
当模型更深时,出现了退化(degradation)现象:随着网络深度的提升,准确性会饱和。
作者认为,如果解决一个任务最适合用K层网络,那么即使我们训练了一个比K深的网络,只要K之后的网络做恒等映射(Identity Mapping),直接返回输入的值,就能取得和K层网络相同的效果。因此,理论上比K深的模型效果不应比K层差,但实验结果是某个任务56层确实比20层差
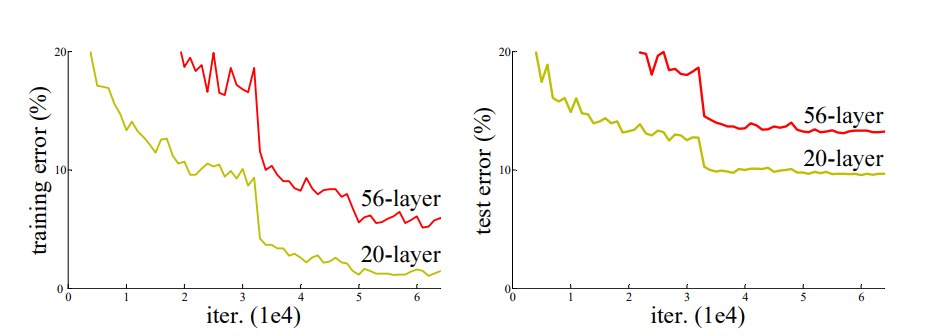
于是作者认为,模型在试图用多个非线性层混合输出一个恒等映射(比如对一个数据先平方再开方之类的吗?),我们应该直接给模型一个恒等映射的能力
残差学习框架
作者引入了残差学习框架,来解决退化问题
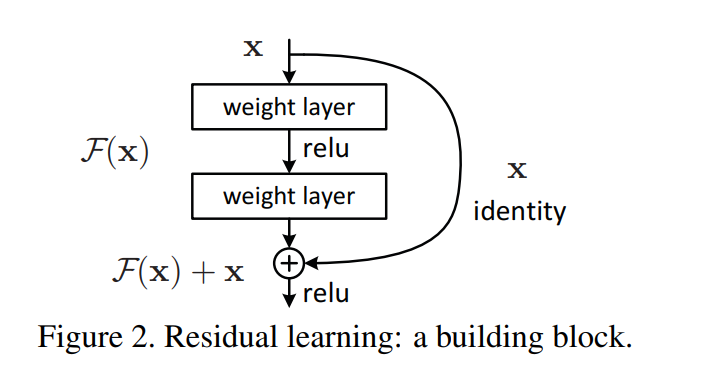
残差网络的核心,是在非线性层基础上加了一个x,从
$$
y = F(x)
$$
变成(当然,新训练出的F(x)和之前是不同的)
$$
y = F(x)+x
$$
使用了这种操作(快捷连接)的网络都可以称作残差神经网络
理论上(万能近似定律),无论是$y=F(x)$还是$y=F(x)+x$,喂入足够的数据,都能拟合出所需的函数,区别是这两个模型的训练难度可能有所差异
通过观察可知,这一层模型是有可能被训练为$y=x$,也就是$F(x)$的输出恒为0,此时实现了恒等映射
维度映射
残差网络中输入和输出的维度应该是相同的,但实践中经常需要改变输出输出的通道数,可以用一个线性投影来匹配维度
$$
y=F(x, {W_i})+W_sx
$$
- zero-padding shortcuts:通过在输入中填充0来增加维度
- projection shortcuts:通过1x1的卷积线性增加或减少维度
作者发现投影效果比零填充要好,但也没有好太多,于是不是必须的
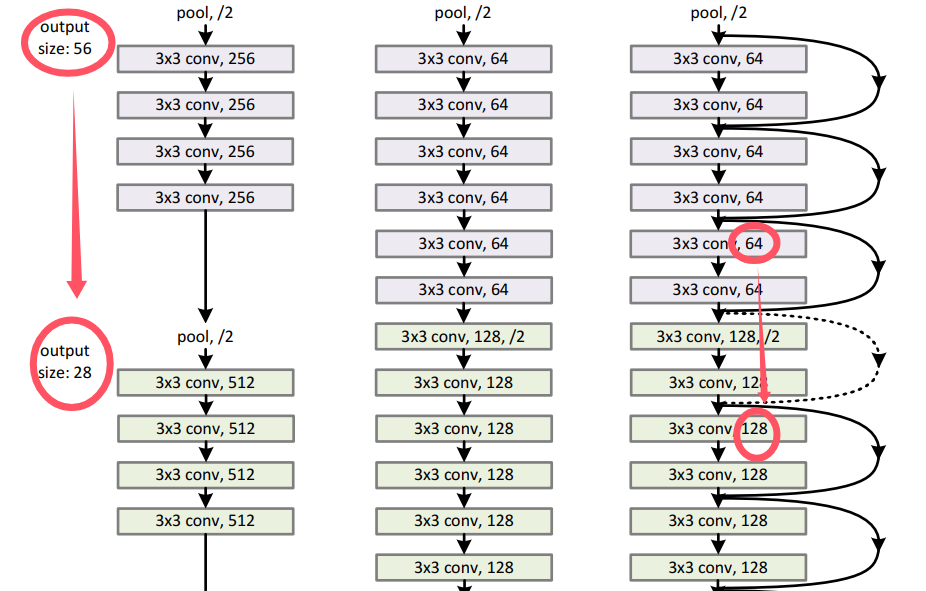
网络架构
- 和VGGNet很类似,使用3x3的滤波器进行卷积
- 当输出的维度减半时,滤波核的数量就跟着翻倍,以维持复杂度
- 每两层网络添加一个快捷连接,以实现残差网络